Упражнение 1153 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1153 учебника 2023-2025 (стр. 228):
Является ли решением уравнения \(x^2 - 2y = 7\) пара значений переменных \(x\) и \(y\):
а) \((5; 8)\);
б) \((-4; -11{,}5)\);
в) \((-1; -3)\);
г) \((1{,}2; -2{,}78)\)?
№1153 учебника 2013-2022 (стр. 227):
Постройте прямую, которая является графиком уравнения \( y - 2{,}5x = c, \) если известно, что она проходит через точку \(K(2;\,-3)\).
Подсказка
№1153 учебника 2023-2025 (стр. 228):
Вспомните:
- Что называют решением линейного уравнения с двумя переменными.
- Степень с натуральным показателем.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение десятичных дробей.
- Сложение десятичных дробей.
№1153 учебника 2013-2022 (стр. 227):
Вспомните:
- Уравнение с двумя переменными, его график.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Координаты точки.
- Умножение десятичных дробей.
Ответ
№1153 учебника 2023-2025 (стр. 228):
\(x^2 - 2y = 7\)
а) \((5; 8)\) - не является решением уравнения.
\(5^2 - 2\cdot8 =7\)
\(25 - 16 =7\)
\(9 = 7\) - неверно.
б) \((-4; -11{,}5)\) - не является решением уравнения.
\(x^2 - 2y = 7\)
\((-4)^2 - 2\cdot(-11{,}5) = 7\)
\(16 + 23 = 7\)
\(39 = 7\) - неверно.
в) \((-1; -3)\) - является решением уравнения.
\((-1)^2 - 2\cdot(-3) = 7\)
\(1 + 6 =7\)
\(7 = 7\) - верно.
г) \((1{,}2; -2{,}78)\) - является решением уравнения.
\((1{,}2)^2 - 2\cdot(-2{,}78) =7\)
\(1{,}44 + 5{,}56 =7\)
\(7 = 7\) - неверно.
Пояснения:
Правила и приёмы, использованные при проверке:
– Подставить в выражение \(x^2 - 2y\) заданные значения \(x\) и \(y\).
– Вычислить полученное арифметическое выражение.
– Сравнить результат с числом 7.
№1153 учебника 2013-2022 (стр. 227):
\( y - 2{,}5x = c, \)
\(K(2;\,-3)\)
\( -3 - 2{,}5\cdot2 = c\)
\(-3 - 5 = c \)
\(c = -8 \)
\( y - 2{,}5x = -8\)
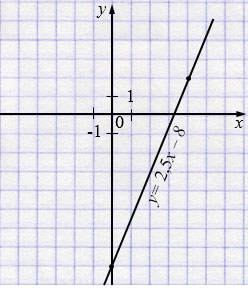
\(y = 2{,}5x - 8 \)
| \(x\) | 0 | 4 |
| \(y\) | -8 | 2 |
Пояснения:
– Линейное уравнение вида
\(y - kx = c\) можно записать как
\(y = kx + c\).
– Подстановка координат точки в уравнение позволяет найти неизвестный параметр \(c\).
– После приведения к виду \(y = kx + b\) прямая строится по двум точкам: удобно взять \(x=0\) и любое другое значение \(x\).
– Точки \((0;-8)\) и \((4;2)\) лежат на искомой прямой и достаточны для её построения.
Вернуться к содержанию учебника