Упражнение 1149 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1149 учебника 2023-2025 (стр. 228):
Изобразите на координатной плоскости множество точек, которое задаёт система неравенств:
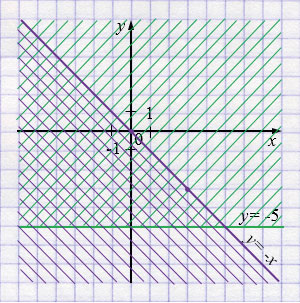
а) \(\displaystyle \begin{cases}y \le -x,\\y \ge -5;\end{cases}\)
б) \(\displaystyle \begin{cases}y \ge x - 2,\\y \le x + 3;\end{cases}\)
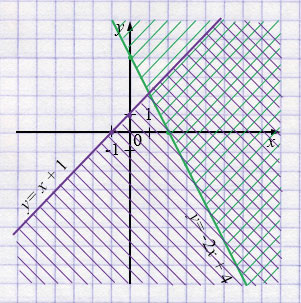
в) \(\displaystyle \begin{cases}y \ge -2x + 4,\\y \le x + 1.\end{cases}\)
№1149 учебника 2013-2022 (стр. 227):
Докажите, что графику уравнения \(3x + 2y = -4\) не принадлежит ни одна точка, у которой обе координаты положительные.
Подсказка
№1149 учебника 2023-2025 (стр. 228):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
№1149 учебника 2013-2022 (стр. 227):
Вспомните:
Ответ
№1149 учебника 2023-2025 (стр. 228):
а) \(\displaystyle \begin{cases}y \le -x,\\y \ge -5\end{cases}\)
\(y = -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
б) \(\displaystyle \begin{cases}y \ge x - 2,\\y \le x + 3\end{cases}\)
\(y = x - 2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | 0 |
\(y = x + 3\)
| \(x\) | 0 | -3 |
| \(y\) | 3 | 0 |

в) \(\displaystyle \begin{cases}y \ge -2x + 4,\\y \le x + 1\end{cases}\)
\(y = -2x + 4\)
| \(x\) | 0 | 2 |
| \(y\) | 4 | 0 |
\(y = x + 1\)
| \(x\) | 0 | -1 |
| \(y\) | 1 | 0 |
Пояснения:
1) Для каждого неравенства проводим соответствующую прямую по двум точкам и определяем, какую сторону штриховать, проверяя точку (например, \((0,0)\)).
2) При знаках «\(\ge\)» и «\(\le\)» граница включается (сплошная линия).
3) Решение системы - пересечение штрихованных областей.
а) Границы: прямая \(y=-x\) и горизонтальная прямая \(y=-5\). Поскольку знак «\(\le\)» у первой, штрихуем область ниже или на линии \(y=-x\). Поскольку знак «\(\ge\)» у второй, штрихуем область выше или на линии \(y=-5\). Итоговая область — полоса между этими прямыми, включая границы.
б) Границы: прямая \(y=x-2\) и прямая \(y=x+3\). Для «\(\ge\)» у первой — штриховка над или на \(y=x-2\). Для «\(\le\)» у второй — штриховка под или на \(y=x+3\). Итоговая область — полоса между этими параллельными прямыми, включая их.
в) Границы: прямая \(y=-2x+4\) и прямая \(y=x+1\). Для «\(\ge\)» у первой — штриховка над или на \(y=-2x+4\). Для «\(\le\)» у второй — штриховка под или на \(y=x+1\). Область — перекрытие двух полуплоскостей, включая границы.
№1149 учебника 2013-2022 (стр. 227):
\(3x + 2y = -4\)
Если \( x > 0\) и \( y > 0\), то
\( 3x > 0\) и \( 2y > 0\), значит,
\( 3x + 2y > 0 \), при этом \( -4 < 0 \), значит, не существует точки с \(x>0\) и \(y>0\) на этом графике.
Пояснения:
– Если переменные \(x\) и \(y\) положительны, то \( 3x\) и \( 2y\) положительны.
– Уравнение требует, чтобы сумма \(3x + 2y\) была равна \(-4\), то есть отрицательна.
– Положительное число не может равняться отрицательному — получаем противоречие.
– Метод «доказательство от противного» позволяет показать невозможность существования такой точки.
Вернуться к содержанию учебника