Упражнение 1178 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1178 учебника 2023-2025 (стр. 230):
Решите графически систему уравнений:
а) \( \begin{cases} y + 3x = 0,\\ x - y = 4,\\ x + y = -2; \end{cases} \)
б) \( \begin{cases} x + y = 1,\\ y - x = 3,\\ 2x + y = 0. \end{cases} \)
№1178 учебника 2013-2022 (стр. 231):
Велосипедист ехал от пункта A до пункта B со скоростью \(10\) км/ч, а от пункта B до пункта C — со скоростью \(15\) км/ч. На весь путь он затратил \(5\) ч. Тот же путь за то же время он мог бы проехать с постоянной скоростью \(12\) км/ч. Сколько часов затратил велосипедист на путь от A до B и сколько на путь от B до C?
Подсказка
№1178 учебника 2023-2025 (стр. 230):
Вспомните:
- Графический метод решения систем уравнений с двумя переменными.
- Уравнения с двумя переменными, их свойства.
- График линейной функции.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№1178 учебника 2013-2022 (стр. 231):
Вспомните:
- Решение задач с помощью систем уравнений.
- Что называют решением системы уравнений.
- Уравнения с двумя переменными, их свойства.
- Способ подстановки при решении систем уравнений.
- Линейное уравнение с одной переменной, его свойства.
- Деление и дроби.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Распределительное свойство умножения.
Ответ
№1178 учебника 2023-2025 (стр. 230):
а) \( \begin{cases} y + 3x = 0,\\ x - y = 4,\\ x + y = -2; \end{cases} \)
\( \begin{cases} y = -3x,\\ y = x - 4,\\ y = -x - 2; \end{cases} \)
\(y = -3x\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | -6 |
\(y = x - 4\)
| \(x\) | 0 | 2 |
| \(y\) | -4 | -2 |
\(y = -x - 2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | -4 |
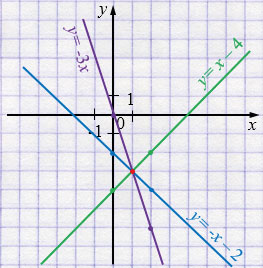
Ответ: \((1;\,-3)\).
б) \( \begin{cases} x + y = 1,\\ y - x = 3,\\ 2x + y = 0. \end{cases} \)
\( \begin{cases} y = 1 - x,\\ y = 3 + x,\\ y = -2x. \end{cases} \)
\(y = 1 - x\)
| \(x\) | 0 | 3 |
| \(y\) | 1 | -2 |
\(y = x + 3\)
| \(x\) | 0 | -3 |
| \(y\) | 3 | 0 |
\(y = -2x\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | -4 |
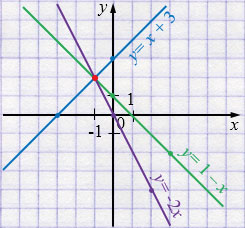
Ответ: \((-1;\,2)\).
Пояснения:
– Графически система уравнений с двумя переменными задаёт пересечение прямых на плоскости.
– Для каждой прямой удобно записать уравнение в явном виде \(y = kx + b\). Для построения прямой достаточно отметить две точки.
– В обоих случаях все три прямые проходят через одну единственную точку, что и является решением системы.
№1178 учебника 2013-2022 (стр. 231):
Пусть \(x\) (ч) и \(y\) (ч) времена движения на участках \(A\to B\) и \(B\to C\) соответственно. Известно, что на весь путь велосипедист затратил 5 ч и тот же путь за то же время он мог бы проехать с постоянной скоростью 12 км/ч.
Составим систему уравнений:
\( \begin{cases} x + y = 5,\\ 10x + 15y = 12\cdot5 \end{cases} \)
\( \begin{cases} x = 5 - y,\\ 10(5 - y) + 15y = 60 \end{cases} \)
\(10(5 - y) + 15y = 60\)
\(50 - 10y + 15y = 60\)
\(5y = 60 - 50\)
\(5y = 10\)
\(y = \frac{10}{2}\)
\(y = 2\)
\(x = 5 - 2 = 3\)
Ответ: велосипедист на путь от A до B затратил 3 ч, на путь от B до C – 2 ч.
Пояснения:
– Обозначили \(x\) и \(y\) как времена на отдельных участках.
– Формула пути для каждого участка: \(S = v\,t\).
– Сумма времен даёт общее время: \(x+y=5\).
– Сумма расстояний на участках \(10x+15y\) должна равняться эквивалентному пути \(60\) км.
– Решили систему линейных уравнений методом подстановки:
- из одного уравнения выражаем одну переменную через другую;
- подставляем это выражение в другое уравнение, получая уравнение с одной переменной;
- решаем полученное уравнение, находим значение первой переменной;
- затем вычисляем вторую переменную, подставляя найденное значение обратно.
Вернуться к содержанию учебника