Задание 2.429 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.429 учебника 2023-2024 (стр. 102):
Вычислите:

№2.429 учебника 2021-2022 (стр. 96):
Найдите частное:
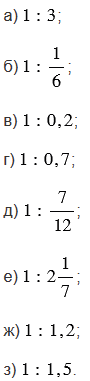
Подсказка
№2.429 учебника 2023-2024 (стр. 102):
Вспомните:
- Порядок выполнения действий.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
- Умножение десятичных дробей.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Основное свойство дроби (сокращение дробей).
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Смешанные числа, действия с ними.
- Неправильные дроби.
- Квадрат числа.
№2.429 учебника 2021-2022 (стр. 96):
Вспомните:
- Взаимно обратные числа.
- Как найти неизвестный множитель.
- Десятичные дроби.
- Смешанные числа.
- Неправильные дроби.
- Сокращение дробей.
- Деление и дроби.
Ответ
№2.429 учебника 2023-2024 (стр. 102):
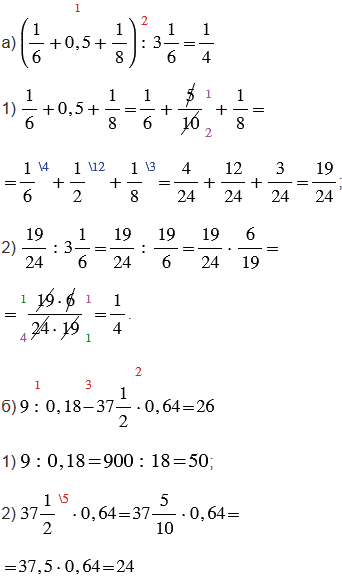
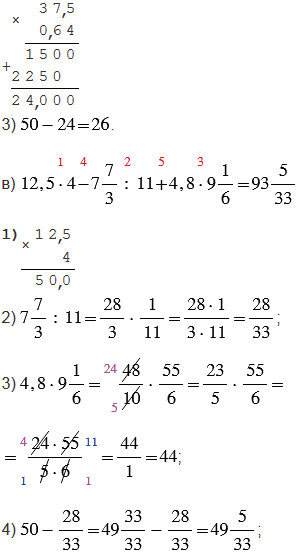
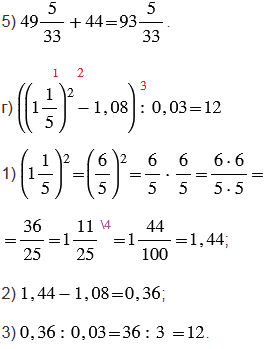
Пояснения:
Действиями первой ступени называют сложение и вычитание чисел, а действиями второй ступени - умножение и деление чисел.
При вычислении значений выражений порядок выполнения действий определяют следующие правила:
1. Если выражение содержит только действия одной ступени и в нем нет скобок, то действия выполняют по порядку слева направо.
2. Если в выражении нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени.
3. Если в выражении есть скобки есть скобки, то сначала выполняют действия в скобках (учитывая правила 1 и 2).
Возведение числа в степень - это пятое арифметическое действие, поэтому стоит учитывать, что если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом - остальные действия, в соответствии с порядком их выполнения.
Красные числа, стоящие сверху над действиями, показывают в каком порядке нужно выполнять действия.
Правила, по которым выполняем вычисления:
1) чтобы сложить (вычесть) две дроби с разными знаменателями, надо: привести данные дроби к общему знаменателю, а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями;
2) чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним;
3) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей;
4) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей;
5) чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу  является число
является число 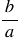 ;
;
6) чтобы выполнить деление смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей;
7) чтобы сложить или вычесть десятичные дроби, нужно записать числа столбиком так, чтобы запятая стояла под запятой. Затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой;
8) чтобы разделить десятичную дробь на десятичную, нужно: перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части;
9) чтобы перемножить две десятичные дроби, надо: записать дроби в столбик, как два натуральных числа не обращая внимание на запятые; умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
При выполнении умножения обыкновенных дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Если при вычислениях получилась неправильная дробь (числитель больше знаменателя), ее нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
№2.429 учебника 2021-2022 (стр. 96):

Пояснения:
Если единицу разделить на какое-то число, то получится число обратное делителю, так как произведение взаимно обратных чисел равно единице.
Помним:
- Обратным числу
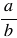 является число
является число  .
. - Если
 - натуральное число, то обратным ему является число
- натуральное число, то обратным ему является число 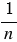 .
.
Если делитель представлен смешанным числом, его нужно преобразовать в неправильную дробь, и если возможно сократить эту дробь. Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Если делитель представлен десятичной дробью, ее нужно преобразовать в обыкновенную дробь, и, если возможно, сократить эту дробь. У обыкновенной дроби в знаменателе столько нулей, сколько знаков после запятой у десятичной дроби.
Если при вычислениях получилась неправильная дробь (числитель больше знаменателя), ее нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
Вернуться к содержанию учебника