Задание 2.366 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.366 учебника 2023-2024 (стр. 94):
Найдите значение выражения:
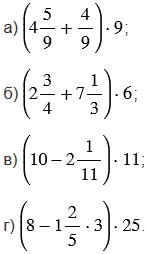
№2.366 учебника 2021-2022 (стр. 87):
1) Для освещения площади используют 29 фонарей, в которых три или две лампочки. Сколько фонарей каждого вида на площади, если всего лампочек 76?
2) К новогоднему празднику для 23 детей купили машинки с тремя и с четырьмя колесами. Сколько машинок каждого вида было куплено, если всего колес 83?
Подсказка
№2.366 учебника 2023-2024 (стр. 94):
Вспомните:
- Распределительное свойство умножения.
- Смешанные числа, действия с ними.
- Неправильные дроби.
- Деление и дроби.
- Деление с остатком.
- Умножение обыкновенных дробей.
- Основное свойство дроби (сокращение дробей).
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Сложение и вычитание дробей с одинаковыми знаменателями.
№2.366 учебника 2021-2022 (стр. 87):
Вспомните:
- Что называют уравнением, его корни.
- Умножение чисел, распределительное свойство умножения.
- Вычитание чисел, его свойства.
Ответ
№2.366 учебника 2023-2024 (стр. 94):
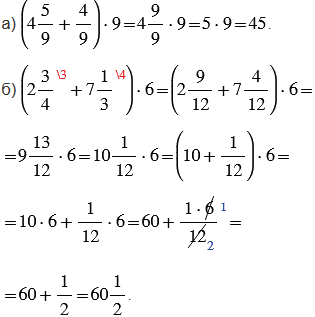
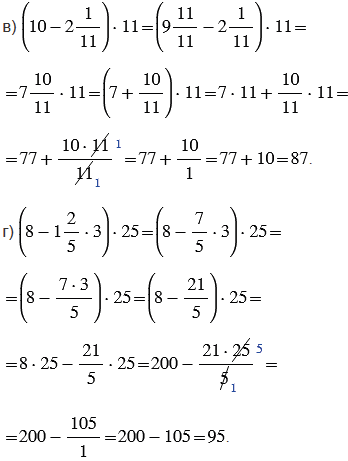
Пояснения:
Чтобы найти значения данных выражений, сначала находим значение выражений в скобках, а затем, используя распределительное свойство умножения, выполняем умножение смешанного числа на натуральное число.
Чтобы умножить смешанное число на натуральное число, используем распределительное свойство умножения, а именно, чтобы умножить смешанное число на натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) сложить полученные результаты.
Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на их наибольший общий делитель. Также помним, дробь, у которой в знаменателе стоит единица, равна своему числителю, а дробь, у которой числитель и знаменатель одинаковые, равна единице.
Чтобы найти сумму смешанных чисел, надо: дробные части этих чисел привести к наименьшему общему знаменателю; отдельно выполнить сложение целых и отдельно дробных частей; при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель), выделить целую часть (когда числитель больше знаменателя) и прибавить ее к полученной целой части;
Чтобы найти разность смешанных чисел, надо: дробные части этих чисел привести к наименьшему общему знаменателю; если дробная часть уменьшаемого больше дробной части вычитаемого, то надо отдельно вычесть целые и отдельно дробные части и результаты сложить; если дробная часть уменьшаемого меньше дробной части вычитаемого, то надо превратить ее в неправильную дробь, уменьшив на единицу целую часть, и отдельно вычесть целые и отдельно дробные части и результаты сложить; при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель);
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо: привести данные дроби к общему знаменателю, а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним.
№2.366 учебника 2021-2022 (стр. 87):
1) Пусть используют  фонарей с тремя лампочками, тогда с двумя лампочками (29 -
фонарей с тремя лампочками, тогда с двумя лампочками (29 -  ) фонарей. В фонарях с тремя лампочками 3
) фонарей. В фонарях с тремя лампочками 3 лампочек, а в фонарях с двумя лампочками 2 • (29 -
лампочек, а в фонарях с двумя лампочками 2 • (29 -  ) лампочек. Всего лампочек 76.
) лампочек. Всего лампочек 76.
Составим уравнение:
3 + 2 • (29 -
+ 2 • (29 -  ) = 76
) = 76
3 + 2 • 29 - 2
+ 2 • 29 - 2 = 76
= 76
(3 - 2
- 2 ) + 58 = 76
) + 58 = 76
 + 58 = 76
+ 58 = 76
 = 76 - 58
= 76 - 58
 = 18 (ф.) - с тремя лампочками.
= 18 (ф.) - с тремя лампочками.
29 -  = 29 - 18 = 11 (ф.) - с двумя лампочками.
= 29 - 18 = 11 (ф.) - с двумя лампочками.
Ответ: 11 фонарей с двумя лампочками и 18 фонарей с тремя лампочками.
2) Пусть купили  машинок с четырьмя колесами, тогда с тремя колесами купили (23 -
машинок с четырьмя колесами, тогда с тремя колесами купили (23 -  ) машинок. У машинок с четырьмя колесами 4
) машинок. У машинок с четырьмя колесами 4 колес, у машинок с тремя колесами 3 • (23 -
колес, у машинок с тремя колесами 3 • (23 -  ) колес. Всего колес 83.
) колес. Всего колес 83.
Составим уравнение:
4 + 3 • (23 -
+ 3 • (23 -  ) = 83
) = 83
4 + 3 • 23 - 3
+ 3 • 23 - 3 = 83
= 83
(4 - 3
- 3 ) + 69 = 83
) + 69 = 83
 + 69 = 83
+ 69 = 83
 = 83 - 69
= 83 - 69
 = 14 (м.) - с четырьмя колесами.
= 14 (м.) - с четырьмя колесами.
23 -  = 23 - 14 = 9 (м.) - с тремя колесами.
= 23 - 14 = 9 (м.) - с тремя колесами.
Ответ: 9 машинок с тремя колесами и 14 машинок с четырьмя колесами.
Пояснения:
Решаем задачи с помощью уравнений.
1) Пусть для освещения площади используют  фонарей с тремя лампочками, тогда, учитывая то, что всего используют 29 фонарей, с двумя лампочками используют (29 -
фонарей с тремя лампочками, тогда, учитывая то, что всего используют 29 фонарей, с двумя лампочками используют (29 -  ) фонарей. Значит, мы имеем
) фонарей. Значит, мы имеем  фонарей по 3 лампочки в каждом, тогда в этих фонарях 3
фонарей по 3 лампочки в каждом, тогда в этих фонарях 3 лампочек, и мы имеем (29 -
лампочек, и мы имеем (29 -  ) фонарей по 2 лампочки в каждом, тогда в этих фонарях 2 • (29 -
) фонарей по 2 лампочки в каждом, тогда в этих фонарях 2 • (29 -  ) лампочек. Всего лампочек 76. Получается, можно составить следующее уравнение:
) лампочек. Всего лампочек 76. Получается, можно составить следующее уравнение:
3 + 2 • (29 -
+ 2 • (29 -  ) = 76.
) = 76.
Используя распределительное свойство умножения относительно сложения, раскрываем скобки, то есть умножаем 2 на каждый компонент в скобках, получаем:
3 + 2 • 29 - 2
+ 2 • 29 - 2 = 76 или, выполнив умножение в левой части уравнения,
= 76 или, выполнив умножение в левой части уравнения,
3 + 58 - 2
+ 58 - 2 = 76.
= 76.
Согласно свойству вычитания числа из суммы, получаем:
(3  - 2
- 2 ) + 58 = 76 или, выполнив вычитание в скобках,
) + 58 = 76 или, выполнив вычитание в скобках,  + 58 = 76.
+ 58 = 76.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
 = 76 - 58,
= 76 - 58,
 = 18.
= 18.
Получается, учитывая обозначения, введенные выше, с тремя лампочками было 18 фонарей, а с двумя лампочками:
29 -  = 29 - 18 = 11 (ф.).
= 29 - 18 = 11 (ф.).
2) Пусть купили  машинок с четырьмя колесами, тогда, учитывая то, что всего купили 23 машинки, с тремя колесами купили (23 -
машинок с четырьмя колесами, тогда, учитывая то, что всего купили 23 машинки, с тремя колесами купили (23 -  ) машинок. Значит, мы имеем
) машинок. Значит, мы имеем  машинки по 4 колеса у каждой, тогда у этих машинок 4
машинки по 4 колеса у каждой, тогда у этих машинок 4 колес, и имеем (23 -
колес, и имеем (23 -  ) машинок по 3 колеса у каждой, тогда у этих машинок 3 • (23 -
) машинок по 3 колеса у каждой, тогда у этих машинок 3 • (23 -  ) колес. Всего колес. Получается, можем составить следующее уравнение:
) колес. Всего колес. Получается, можем составить следующее уравнение:
4 + 3 • (23 -
+ 3 • (23 -  ) = 83.
) = 83.
Используя распределительное свойство умножения относительно сложения, раскрываем скобки, то есть умножаем 3 на каждый компонент в скобках, получаем:
4 + 3 • 23 - 3
+ 3 • 23 - 3 = 83 или, выполнив умножение в левой части уравнения,
= 83 или, выполнив умножение в левой части уравнения,
4 + 69 - 3
+ 69 - 3 = 83.
= 83.
Согласно свойству вычитания числа из суммы, получаем:
(4 - 3
- 3 ) + 69 = 83 или, выполнив вычитание в скобках,
) + 69 = 83 или, выполнив вычитание в скобках,  + 69 = 83.
+ 69 = 83.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
 = 83 - 69
= 83 - 69
 = 14.
= 14.
Получается, учитывая обозначения, введенные выше, с четырьмя колесами было 14 машинок, а с тремя колесами:
23 -  = 23 - 14 = 9 (м.).
= 23 - 14 = 9 (м.).
Вернуться к содержанию учебника