Задание 300 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№300 учебника 2013-2022 (стр. 89):
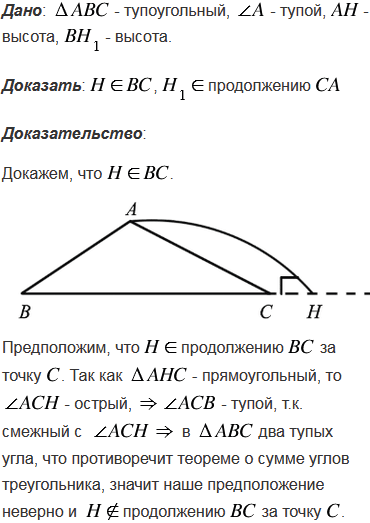
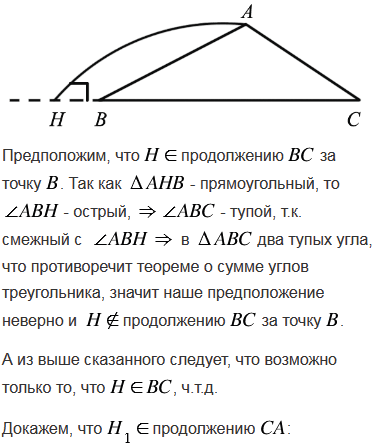
Докажите, что тупоугольном треугольнике основание высоты, проведённой из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведённых из вершин острых углов, - на продолжениях сторон.
№300 учебника 2023-2024 (стр. 87):
Даны отрезки Р1Q1, Р2Q2 и Р3Q3. Постройте треугольник АВС так, чтобы:
а) АВ = Р1Q1, ВС = Р2Q2, СА = 2Р3Q3;
б) АВ = 2Р1Q1, ВС = Р2Q2, СА = 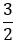 Р3Q3.
Р3Q3.
Всегда ли задача имеет решение?
Подсказка
№300 учебника 2013-2022 (стр. 89):
Вспомните:
- Что такое угол.
- Виды углов.
- Какие углы называются смежными.
- Что такое треугольник.
- Какой треугольник называется тупоугольным.
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
- Что такое высота.
- Теорему о сумме углов треугольника.
№300 учебника 2023-2024 (стр. 87):
Вспомните:
- Какая фигура называется треугольником.
- Как построить отрезок, равный данному.
- Как построить треугольник по трем сторонам.
- Неравенство треугольника.
- Как построить середину отрезка.
Ответ
№300 учебника 2013-2022 (стр. 89):






№300 учебника 2023-2024 (стр. 87):
а) Дано: отрезки Р1Q1, Р2Q2 и Р3Q3.
Построить 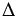 АВС такой, что
АВС такой, что
АВ = Р1Q1, ВС = Р2Q2, СА = 2Р3Q3.
Решение:
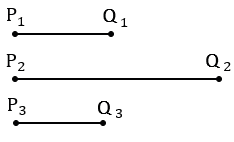
Ответ:
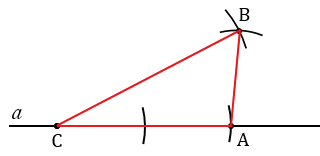
Задача имеет решение, если выполняется неравенство треугольника.
б) Дано: отрезки Р1Q1, Р2Q2 и Р3Q3.
Построить 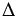 АВС такой, что
АВС такой, что
АВ = 2Р1Q1, ВС = Р2Q2, СА = 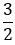 Р3Q3.
Р3Q3.
Решение:
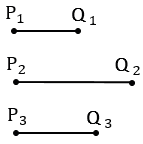
Ответ:
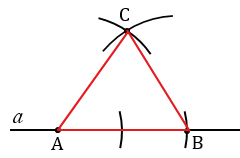
Задача имеет решение, если выполняется неравенство треугольника.
Пояснения:
а) С помощью линейки проводим прямую 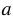 и на ней с помощью циркуля отложим отрезок СА = 2Р3Q3. Для этого произвольно на прямой
и на ней с помощью циркуля отложим отрезок СА = 2Р3Q3. Для этого произвольно на прямой 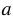 ставим точку С, с помощью циркуля измеряем отрезок Р3Q3 и строим окружность с центром в точке С радиуса Р3Q3, переставляем острие циркуля в точку пересечения полученной окружности с прямой
ставим точку С, с помощью циркуля измеряем отрезок Р3Q3 и строим окружность с центром в точке С радиуса Р3Q3, переставляем острие циркуля в точку пересечения полученной окружности с прямой 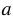 и еще раз чертим окружность радиуса Р3Q3 (полностью окружности строить необязательно, смотри, выделенное красным цветом). Точку пересечения второй окружности с прямой
и еще раз чертим окружность радиуса Р3Q3 (полностью окружности строить необязательно, смотри, выделенное красным цветом). Точку пересечения второй окружности с прямой 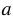 обозначаем А.
обозначаем А.

Далее строим окружности с центрами в точках А и С радиусами Р1Q1 и Р2Q2 соответственно (полностью окружности строить необязательно, смотри, выделенное синим и зеленым цветом). Точку пересечения данных окружностей обозначаем В.
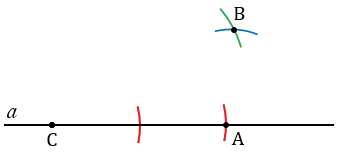
С помощью линейки соединяем точки А и В, С и В. Получаем 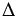 АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СА = 2Р3Q3.
АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СА = 2Р3Q3.

Данная задача будет иметь решение, если выполняется неравенство треугольника, т.е. каждая сторона треугольника должна быть меньше суммы двух других сторон.
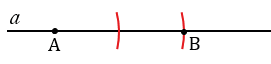
б) С помощью линейки проводим прямую 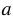 и на ней с помощью циркуля отложим отрезок АВ = 2Р1Q1. Для этого произвольно на прямой
и на ней с помощью циркуля отложим отрезок АВ = 2Р1Q1. Для этого произвольно на прямой 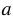 ставим точку А, с помощью циркуля измеряем отрезок Р1Q1 и строим окружность с центром в точке А радиуса Р1Q1, переставляем острие циркуля в точку пересечения полученной окружности с прямой
ставим точку А, с помощью циркуля измеряем отрезок Р1Q1 и строим окружность с центром в точке А радиуса Р1Q1, переставляем острие циркуля в точку пересечения полученной окружности с прямой 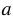 и еще раз чертим окружность радиуса Р1Q1 (полностью окружности строить необязательно, смотри, выделенное красным цветом). Точку пересечения второй окружности с прямой
и еще раз чертим окружность радиуса Р1Q1 (полностью окружности строить необязательно, смотри, выделенное красным цветом). Точку пересечения второй окружности с прямой 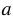 обозначаем В.
обозначаем В.
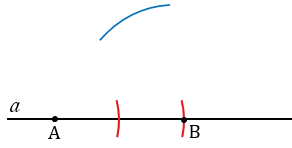
Далее строим окружность с центром в точке В радиуса Р2Q2 (полностью окружность строить необязательно, смотри, выделенное синим цветом).
Чтобы построить СА = 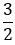 Р3Q3 нужно найти середину отрезка Р3Q3. Для этого с помощью циркуля строим две окружности радиуса Р3Q3 с центрами в точках Р3 и Q3 (полностью окружности строить необязательно, смотри, выделенное зеленым и фиолетовым цветом).
Р3Q3 нужно найти середину отрезка Р3Q3. Для этого с помощью циркуля строим две окружности радиуса Р3Q3 с центрами в точках Р3 и Q3 (полностью окружности строить необязательно, смотри, выделенное зеленым и фиолетовым цветом).
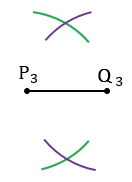
Получим две точки пересечения данных окружностей, через них с помощью линейки проводим прямую, которая пересечет отрезок Р3Q3 в центре - точке О. Затем измеряем отрезок Р3О и откладываем его от точки Q3 на продолжении луча Р3Q3. Для этого с помощью линейки продолжаем луч Р3Q3 и строим окружность с центром в точке Q3 радиуса Р3О (полностью окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения данной окружности с лучом Р3Q3 обозначаем E.
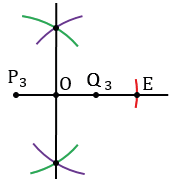
Далее с помощью циркуля измеряем отрезок Р3Е и строим окружность радиуса Р3Е с центром в точке А (полностью окружность строить необязательно, смотри, выделенное зеленым цветом).
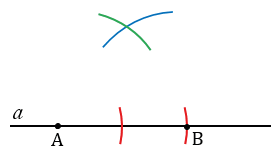
Точку пересечения окружностей с центрами в точках А и В, обозначаем С и соединяем ее с точками А и В с помощью линейки. Получаем  АВС такой, что АВ = 2Р1Q1, ВС = Р2Q2, СА =
АВС такой, что АВ = 2Р1Q1, ВС = Р2Q2, СА = 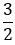 Р3Q3.
Р3Q3.

Данная задача будет иметь решение, если выполняется неравенство треугольника, т.е. каждая сторона треугольника должна быть меньше суммы двух других сторон.
Вернуться к содержанию учебника