Неравенства с двумя переменными и их системы / Неравенства / Справочник по математике 5-9 класс

Определение:

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое равенство

Рассмотрим, как изображается на координатной плоскости множество решений неравенства с двумя переменными.

Пример 1.

Изобразим на координатной плоскости множество решений неравенства \(4x+2y>6\).

Заменим его равносильным неравенством:

\(2y>-4x+6\) \(|:2\)

\(y>-2x+3\).

Прямая \(y=-2x+3\) разделит плоскость на две полуплоскости, при этом неравенством \(4x+2y>6\) задается множество точек координатной плоскости, расположенных выше прямой \(y=-2x+3\), т.е. открытая полуплоскость (полуплоскость без граничной прямой). Чтобы показать, что прямая \(y=-2x+3\) не принадлежит полуплоскости, на рисунке ее будем изображать штриховой линией.

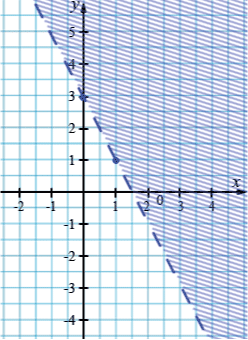
Заметим, что координаты точек заштрихованной полуплоскости удовлетворяют неравенству \(4x+2y>6\), а координаты точек второй полуплоскости неравенству \(4x+2y<6.\)

Пример 2.

Изобразим на координатной плоскости множество решений неравенства \(y\leq-x^2-5x\). Для этого построим график уравнения \(y=-x^2-5x\). Тогда решениями данного неравенства будут координаты точек, принадлежащих параболе \(y=-x^2-5x\), и координаты точек, расположенных ниже ее.

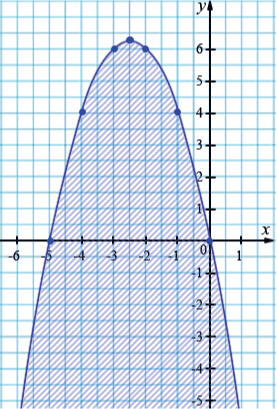
Определение

Решением системы неравенств с двумя переменными называют такую пару чисел, при подстановке которой каждое неравенство системы превращается в верное числовое неравенство, то есть выполняются все неравенства одновременно. Множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в нее неравенств.

На координатной плоскости множество решений системы неравенств изображается множеством точек, представляющих общую часть множеств, задаваемых неравенствами, входящими в систему.