Упражнение 450 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 134

\(ax + by > c\)

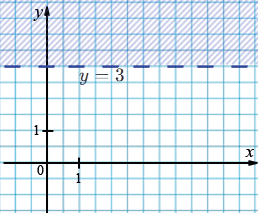
а) \(a = 0,\ b = 1,\ c = 3:\)

\(0\cdot x + 1\cdot y > 3,\)

\(y > 3.\)

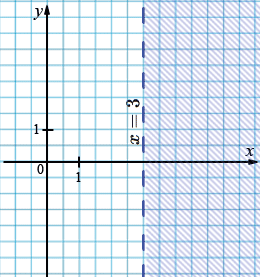
б) \(a = 1,\ b = 0,\ c = 3\).

\(1\cdot x + 0\cdot y > 3\)

\(x > 3.\)

Пояснения:

Общие правила:

1) Равенство вида \(ax + by = c\) задаёт прямую на координатной плоскости.

2) Неравенства \(ax + by > c\) или \(ax + by < c\) задают одну из полуплоскостей, на которую эта прямая делит плоскость.

3) При строгом неравенстве прямая не входит в множество решений.

Пояснение к пункту а)

Так как \(a = 0\), то переменная \(x\) исчезает из неравенства. Получается условие только на \(y\):

\[y > 3.\]

Это все точки выше горизонтальной прямой \(y = 3\). Прямая не входит в решение, так как знак строгий.

Пояснение к пункту б)

Так как \(b = 0\), переменная \(y\) исчезает. Получаем неравенство:

\[x > 3.\]

Это все точки правее вертикальной прямой \(x = 3\). Прямая не входит, потому что знак строгий.

Таким образом, в обоих случаях необходимо построить прямую и выделить соответствующую полуплоскость.