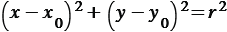Уравнение окружности
Выведем уравнение окружности радиуса 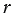 с центром
с центром 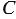 в заданной прямоугольной системе координат. Пусть точка
в заданной прямоугольной системе координат. Пусть точка 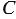 имеет координаты
имеет координаты 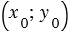 :
:
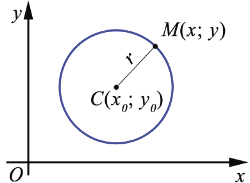
Расстояние от произвольной точки 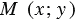 до точки
до точки 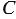 вычисляется по формуле
вычисляется по формуле 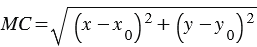 . Если точка
. Если точка 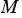 лежит на данной окружности, то
лежит на данной окружности, то 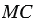 =
= 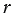 ,
, 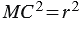 , т.е. координаты точки
, т.е. координаты точки 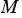 удовлетворяют уравнению
удовлетворяют уравнению
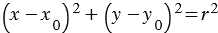 (1)
(1)
Если же точка 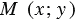 не лежит на данной окружности, то
не лежит на данной окружности, то 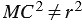 , и, значит, координаты точки
, и, значит, координаты точки 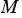 не удовлетворяют уравнению (1).
не удовлетворяют уравнению (1).
|
В прямоугольной системе координат уравнение окружности радиуса
|
Частный случай: уравнение окружности радиуса 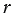 с центром в начале координат:
с центром в начале координат: 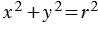
Задача
Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.
Дано: окр.(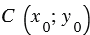 ),
), 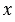 0 = -3,
0 = -3, 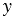 0 = 4,
0 = 4, 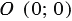
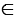 окр.(
окр.(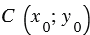 )
)
Найти: уравнение окр.(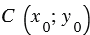 )
)
Решение:
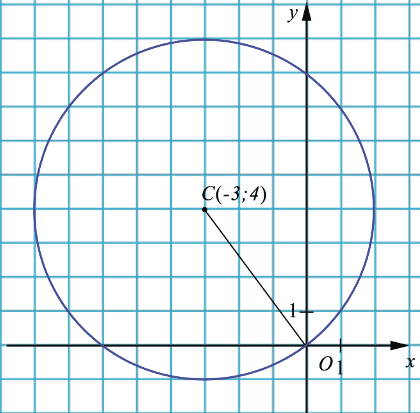
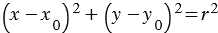 , следовательно, для данной окружности имеем, что
, следовательно, для данной окружности имеем, что 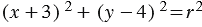 (2).
(2).
Найдем 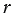 : т.к.
: т.к. 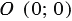
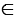 окр.(
окр.(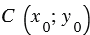 ), т.е. координаты точки
), т.е. координаты точки 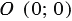 удовлетворяют уравнению (2):
удовлетворяют уравнению (2):
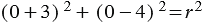 .
.
Отсюда 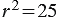 или
или 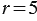 .
.
Итак, искомое уравнение окружности имеет вид 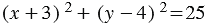 .
.
Раскроем скобки и приведем подобные члены, получим, что: 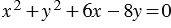 . Полученное уравнение также является уравнением данной окружности.
. Полученное уравнение также является уравнением данной окружности.
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Взаимное расположение двух окружностей
Правило встречается в следующих упражнениях:
7 класс
Задание 1000, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1002, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1264, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1265, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1065, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1066, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1068, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9 класс
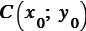 имеет вид:
имеет вид: