Применение векторов к решению задач

Задача 1

Точка С  - середина отрезка АВ, а О - произвольная точка плоскости. Доказать, что = ( + ).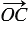

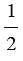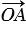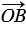Дано: С  - середина отрезка АВ, О - произвольная точка плоскости

Доказать: = ( + )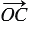

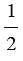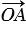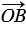Доказательство:

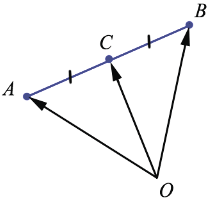
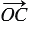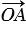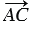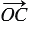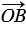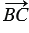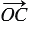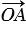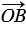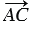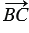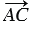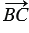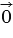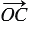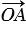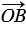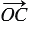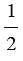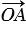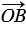По правилу треугольника = + , = + . Складывая эти равенства, получаем: 2 = +  + ( + ). Так как точка С  - середина отрезка АВ, то + = . Таким образом, 2 = + , или = ( + ), что и требовалось доказать.

Задача 2

Доказать, что прямая, проведённая через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

Дано: ABCD - трапеция, М и N - середины оснований ВС и AD соответственно, О = AB 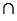CD

Доказать: O 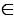MN

Доказательство:

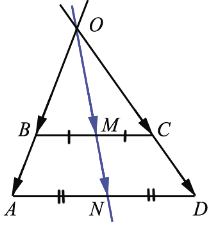
OADOВС (по первому признаку подобия треугольников, так как 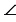OBC = 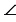OAD и 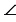OCB = 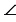ODA как соответственные углы при параллельных прямых ВС и AD секущими AO и OD соответственно), следовательно, .

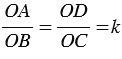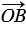
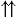
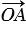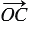
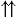
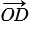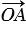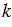
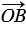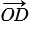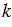
Так как и (данные векторы являются сонаправленными, так как лежат на одной прямой и направлены в одинаково), то = , = 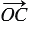.      (1)

Точка М - середина отрезка ВС, поэтому 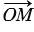= 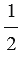( 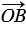+ 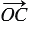). Аналогично 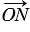= 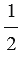( 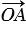+ 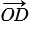) (см. задачу 1).

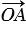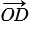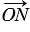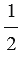
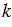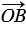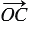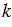
Подставив в это равенство выражения (1) для и , получим: = ( + ) =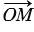, следовательно, векторы 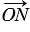и 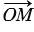коллинеарны, и значит, O 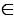MN, что и требовалось доказать.