Законы сложения векторов. Правило параллелограмма
Теорема
|
Для любых векторов 10. 20. ( |
Доказательство
Дано:  ,
,  и
и  .
.
Доказать: 10.  +
+  =
=  +
+  ; 20. (
; 20. ( +
+  ) +
) +  =
=  + (
+ ( +
+  ).
).
Доказательство:
10. Пусть векторы  и
и  коллинеарны.
коллинеарны.
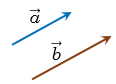
От произвольной точки А отложим векторы  =
=  и
и  =
=  , т.е. векторы
, т.е. векторы  и
и  будут лежать на одной прямой и на той же прямой от точки А отложим векторы
будут лежать на одной прямой и на той же прямой от точки А отложим векторы 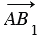 =
=  и
и 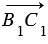 =
=  .
.
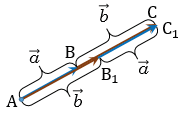
 +
+  =
= 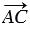 ,
,  +
+  =
= 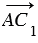 , тогда
, тогда 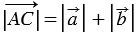 ,
, 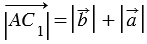 , при этом
, при этом 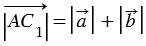 , так как модуль вектора - это длина отрезка, следовательно,
, так как модуль вектора - это длина отрезка, следовательно, 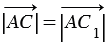 . Поэтому точки С и С1 совпадают, значит,
. Поэтому точки С и С1 совпадают, значит, 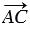 =
= 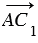 (по определению равных векторов), значит,
(по определению равных векторов), значит,  +
+  =
=  +
+  .
.
Пусть теперь векторы  и
и  не коллинеарны.
не коллинеарны.
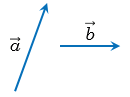
От произвольной точки А отложим векторы  =
=  и
и 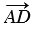 =
=  и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы
и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы  и
и 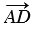 сонаправлены, следовательно,
сонаправлены, следовательно,  =
= 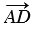 =
=  (по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы
(по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы 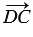 и
и  сонаправлены, следовательно,
сонаправлены, следовательно, 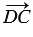 =
=  =
=  .
.
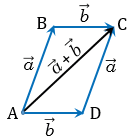
По правилу треугольника 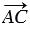 =
=  +
+  =
=  +
+  . Аналогично
. Аналогично 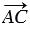 =
= 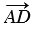 +
+ 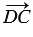 =
=  +
+  , поэтому
, поэтому  +
+  =
=  +
+  .
.
20. От произвольной точки А отложим вектор  =
=  , от точки В - вектор
, от точки В - вектор  =
=  , а от точки С - вектор
, а от точки С - вектор 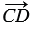 =
=  .
.
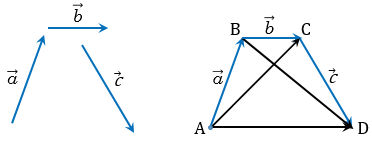
Применяя правило треугольника, получим:
( +
+  ) +
) +  = (
= ( +
+  ) +
) + 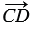 =
= 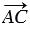 +
+ 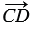 =
= 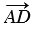 ,
,
 + (
+ ( +
+  ) =
) =  + (
+ ( +
+ 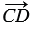 ) =
) =  +
+ 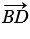 =
= 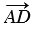 .
.
Следовательно, ( +
+  ) +
) +  =
=  + (
+ ( +
+  ).
).
Теорема доказана.
Правило параллелограмма
Чтобы сложить неколлинеарные векторы  и и  , нужно отложить от какой-нибудь точки А векторы , нужно отложить от какой-нибудь точки А векторы  = =  и и 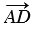 = =  и построить параллелограмм АВСD. Тогда вектор и построить параллелограмм АВСD. Тогда вектор 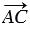 равен равен  + +  . . |

Советуем посмотреть:
Откладывание вектора от данной точки
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 762, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 784, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 808, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 907, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 908, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 909, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник