Произведение вектора на число
Определение
Произведением ненулевого вектора 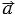 на число на число 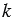 называется такой вектор называется такой вектор 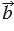 , длина которого равна , длина которого равна  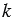 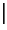  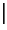 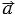 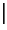 , причём векторы , причём векторы 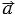 и и 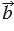 сонаправлены при сонаправлены при 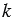 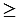 0 и противоположно направлены при 0 и противоположно направлены при 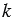 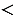 0. Произведением нулевого вектора на любое число считается нулевой вектор. 0. Произведением нулевого вектора на любое число считается нулевой вектор. |
Произведение вектора 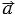 на число
на число 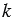 обозначается так:
обозначается так: 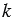
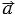
Из определения следует, что:
- произведение любого вектора на число нуль есть нулевой вектор;
- для любого числа
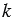 и любого вектора
и любого вектора 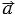 векторы
векторы 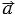 и
и 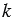
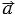 коллинеарны.
коллинеарны.
Основные свойства умножения вектора на число:
|
Для любых чисел 10. ( 20. ( 30. |
Замечание
Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение 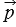 = 2(
= 2(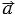 -
- 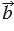 ) + (
) + (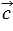 +
+ 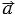 ) - 3(
) - 3(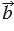 -
- 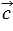 +
+ 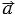 ) можно преобразовать так:
) можно преобразовать так:
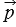 = 2
= 2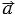 - 2
- 2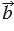 +
+ 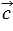 +
+ 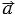 - 3
- 3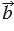 + 3
+ 3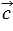 - 3
- 3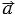 = - 5
= - 5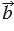 + 4
+ 4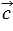 .
.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 775, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 803, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 806, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 903, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1074, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1368, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
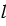 и любых векторов
и любых векторов