Сумма нескольких векторов
Правило сложения нескольких векторов:
| Первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. |
Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
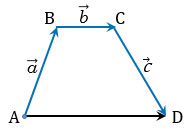
На рисунке выше показано построение векторов 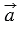 ,
, 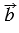 и
и 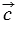 : от произвольной точки А последовательно отложены три вектора
: от произвольной точки А последовательно отложены три вектора 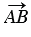 =
= 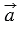 ,
, 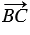 =
= 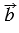 ,
, 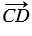 =
= 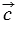 , которые в сумме дают вектор
, которые в сумме дают вектор 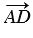 , т.е.
, т.е. 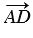 =
= 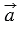 +
+ 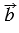 +
+ 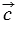 .
.
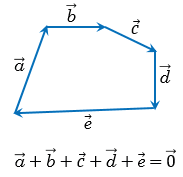
Аналогично можно построить сумму любого числа векторов. На рисунке ниже показано построение суммы шести векторов.
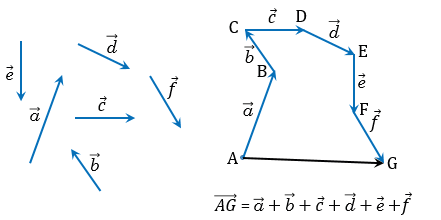
Данное правило построения суммы нескольких векторов называется правилом многоугольника (рисунок поясняет название).
Правило многоугольника
Если А1, А2, ..., Аn - произвольные точки плоскости, то 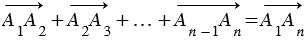 (на рисунке ниже (на рисунке ниже 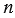 = 9). = 9). |
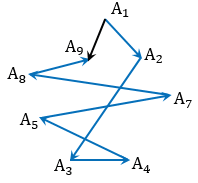
Это правило справедливо для любых точек А1, А2, ..., Аn, в частности в том случае когда некоторые из них совпадают. Если совпадают начало первого вектора и конец последнего, то сумма данных векторов равна нулевому вектору. На рисунке ниже совпадают начало первого вектора 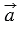 и конец последнего вектора
и конец последнего вектора  .
.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 755, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 761, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 766, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 778, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 789, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник