Сумма двух векторов
Рассмотрим два вектора 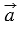 и
и 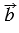 и найдем их сумму. Для этого отметим произвольную точку А и отложим от этой точки вектор
и найдем их сумму. Для этого отметим произвольную точку А и отложим от этой точки вектор 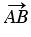 , равный
, равный 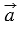 . Затем от точки В отложим вектор
. Затем от точки В отложим вектор 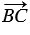 , равный
, равный 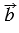 . Вектор
. Вектор 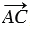 , равный вектору
, равный вектору 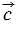 , называется суммой векторов
, называется суммой векторов 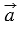 и
и 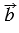 .
.
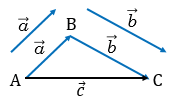
Суммой двух векторов 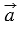 и и 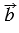 называется третий вектор называется третий вектор 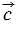 , проведенный из начала вектора , проведенный из начала вектора 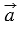 к концу вектора к концу вектора 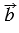 , если начало вектора , если начало вектора 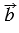 совпадает с концом вектора совпадает с концом вектора 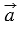 . . |
Данное правило сложения векторов называется правилом треугольника (рисунок поясняет это название).
Сумма векторов 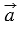 и
и 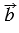 обозначается так:
обозначается так: 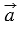 +
+ 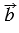 .
.
Результат 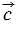 сложения (сумма) векторов сложения (сумма) векторов 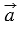 и и 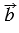 не зависит от выбора точки, от которой откладывается вектор не зависит от выбора точки, от которой откладывается вектор 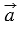 . . |
Доказательство
Дано: 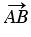 =
= 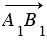 ,
, 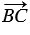 =
= 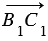 .
.
Доказать: 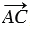 =
= 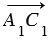 .
.
Доказательство:
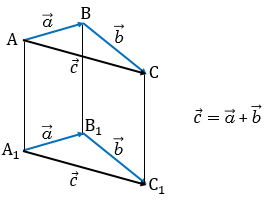
Допустим, что точки А, В, А1, точки В, С, В1 и точки А, С, А1 не лежат на одной прямой. Из равенства 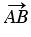 =
= 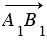 следует, что стороны АВ и А1В1 четырехугольника АВВ1А1 равны и параллельны, т.к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник - параллелограмм. Поэтому АА1 = ВВ1, значит, и
следует, что стороны АВ и А1В1 четырехугольника АВВ1А1 равны и параллельны, т.к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник - параллелограмм. Поэтому АА1 = ВВ1, значит, и 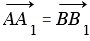 . Аналогично из равенства
. Аналогично из равенства 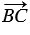 =
= 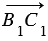 следует, что четырехугольник ВСС1В1 - параллелограмм. Поэтому
следует, что четырехугольник ВСС1В1 - параллелограмм. Поэтому 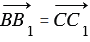 .
.
Итак, 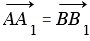 ,
, 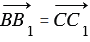 , следовательно,
, следовательно, 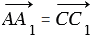 . Поэтому АА1С1С - параллелограмм, и, значит,
. Поэтому АА1С1С - параллелограмм, и, значит, 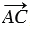 =
= 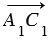 . Что и требовалось доказать.
. Что и требовалось доказать.
Складывая по правилу треугольника произвольный вектор 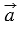 с нулевым вектором, получаем, что для любого вектора
с нулевым вектором, получаем, что для любого вектора 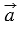 справедливо равенство
справедливо равенство 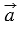 +
+ 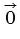 =
= 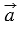 .
.
Правило треугольника можно сформулировать и так:
Если А, В и С - произвольные точки, то 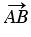 + + 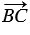 = = 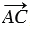 . . |
Данное правило справедливо для произвольных точек А, В и С, даже в том случае, когда две из них или даже все три совпадают.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 758, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 769, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 772, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 773, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 782, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 784, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 789, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 804, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник