Вычитание векторов
Разность векторов 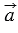 и и 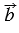 - вектор, сумма которого с вектором - вектор, сумма которого с вектором 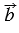 равна вектору равна вектору 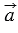 . . |
Разность векторов 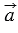 и
и 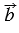 обозначается так:
обозначается так: 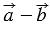 .
.
Задача на построение разности векторов (1 способ)
Даны векторы 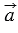 и
и 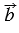 . Построить вектор
. Построить вектор 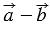 .
.
Дано: 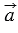 и
и 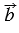 .
.
Построить: 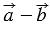 .
.
Решение:
От произвольной точки О откладываем векторы 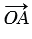 =
= 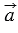 и
и 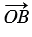 =
= 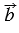 .
.
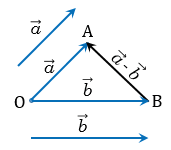
По правилу треугольника 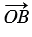 +
+ 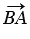 =
= 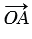 или
или 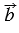 +
+ 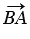 =
= 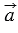 , то есть сумма векторов
, то есть сумма векторов 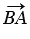 и
и 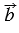 равна
равна 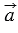 . По определению разности векторов это означает, что
. По определению разности векторов это означает, что 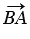 =
= 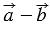 , следовательно, вектор
, следовательно, вектор 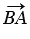 - искомый.
- искомый.
Противоположный вектор
Пусть 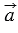 - произвольный ненулевой вектор.
- произвольный ненулевой вектор.
Вектор 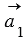 называется противоположным вектору называется противоположным вектору 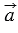 , если векторы , если векторы 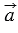 и и 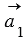 имеют равные длины и противоположно направлены. имеют равные длины и противоположно направлены. |
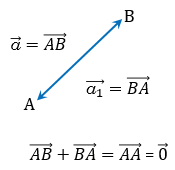
Вектор 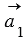 =
= 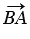 является противоположным вектору
является противоположным вектору 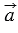 =
= 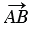 . Вектором, противоположным нулевому вектору, считается нулевой вектор.
. Вектором, противоположным нулевому вектору, считается нулевой вектор.
Вектор, противоположный вектору 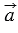 , обозначается так:
, обозначается так: 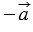 .
.
Сумма противоположных векторов 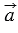 и и 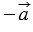 равна нулевому вектору, т.е. равна нулевому вектору, т.е. 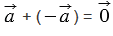 . . |
Теорема
Для любых векторов 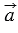 и и 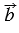 справедливо равенство справедливо равенство 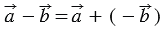 . . |
Доказательство
Дано: 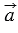 и
и 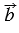 .
.
Доказать: 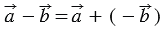 .
.
Доказательство:
По определению разности векторов 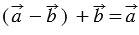 . Прибавим к обеим частям этого равенства вектор
. Прибавим к обеим частям этого равенства вектор 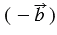 , получим:
, получим:
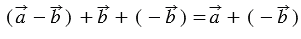 или
или 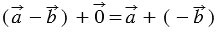 (т.к.
(т.к. 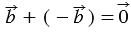 ), следовательно,
), следовательно, 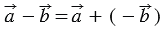 . Теорема доказана.
. Теорема доказана.
Задача на построение разности векторов (2 способ)
Даны векторы 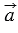 и
и 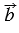 . Построить вектор
. Построить вектор 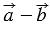 .
.
Дано: 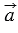 и
и 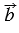 .
.
Построить: 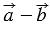 .
.
Решение:
От произвольной точки О откладываем векторы 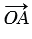 =
= 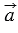 . Затем от точки А отложим
. Затем от точки А отложим 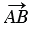 =
=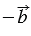 .
.
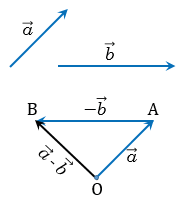
По теореме о разности векторов 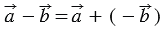 , поэтому
, поэтому 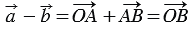 , следовательно, вектор
, следовательно, вектор 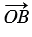 - искомый.
- искомый.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 756, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 776, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 905, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 907, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 925, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1050, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1069, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник