Средняя линия трапеции

$$  Средняя линия трапеции   - это отрезок, который соединяет середины её боковых сторон.

Теорема

Доказательство

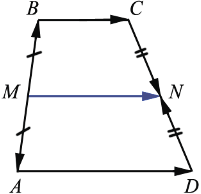
Дано: ABCD - трапеция, MN - средняя линия ABCD

Доказать: MN 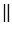AD,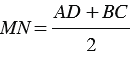

Доказательство:

По правилу многоугольника 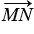= 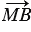+ + 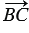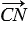и 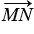= 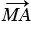+ + 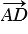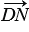. Сложив эти равенства, получим:

2 = ( + ) + ( + ) + ( + ).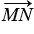

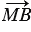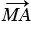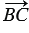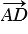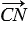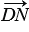Но M и N - середины сторон АВ и CD, поэтому 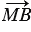+ 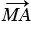=  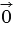и 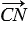 + 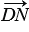=  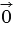(так как сумму составляют противоположные векторы, а сумма противоположных векторов равна нулевому вектору) . Следовательно, 2 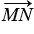= 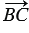+ 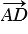, откуда = ( + ).

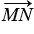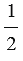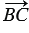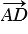Так как векторы 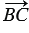и 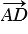сонаправлены, то векторы 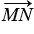и 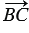также сонаправлены, а длина вектора ( 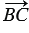+ 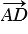) равна AD + ВС. Отсюда следует, что MN 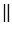AD, 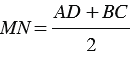. Теорема доказана.