Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения -  с  градусом, записывают так 1$°$.

Градусная мера угла - это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

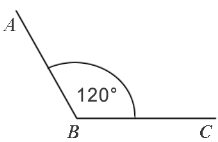
Градусная мера угла ABC равна 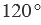. Говорят: "Угол ABC равен 120 градусам". Пишут: .

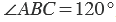Транспортир - это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .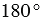

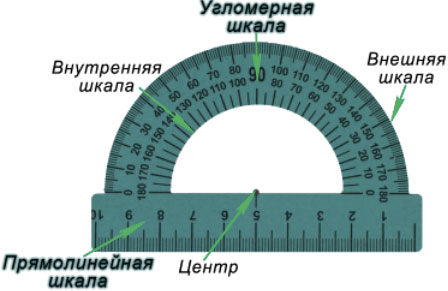
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

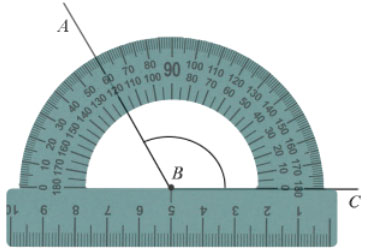
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .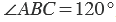

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеет меньшую градусную меру.
• Развернутый угол равен .
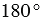• Неразвернутый угол меньше .
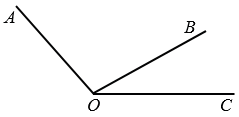
• Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

         АОС = АОВ + ВОС.

Виды углов:

1. Острый угол - угол, градусная мера которого меньше 90°.

2. Прямой угол - угол, градусная мера которого равна 90°.

3. Тупой угол - угол, градусная мера которого больше 90°, но меньше 180°.

4. Развернутый угол - угол, градусная мера которого равна 180°.

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90⁰.

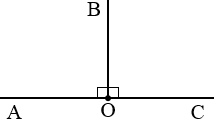
АОС - развернутый, ОВ - биссектриса, АОВ = ВОС = 90⁰.