Прямоугольный параллелепипед. Пирамида.

Многогранник - это поверхность, составленная из многоугольников. Грани многогранника - это многоугольники, из которых он составлен. При этом никакие две соседние грани многогранника не лежат в одной плоскости. Стороны граней - это рёбра многогранника, а их концы - это его вершины. На рисунке ниже изображены многогранники.

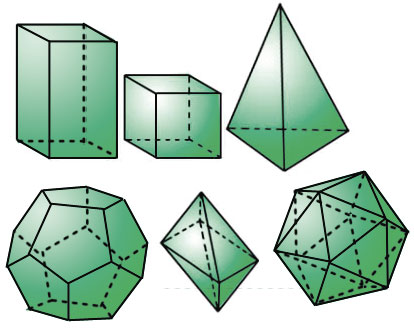
Один из самых простых многогранников - это прямоугольный параллелепипед. Он составлен из шести прямоугольников, т.е. он ограничен шестью гранями.

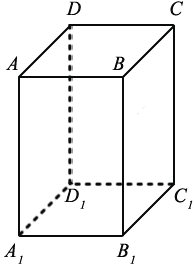
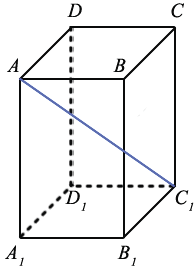
ABCDA₁B₁C₁D₁  - прямоугольный параллелепипед. Ребра прямоугольного параллелепипеда  - это стороны граней (в нашем случае: AB, BC, CD, DA, A₁B₁, B₁C₁, C₁D₁, D₁A₁, AA₁, BB₁, CC₁, DD₁ ). А его вершины - это вершины граней (в нашем случае: A, B, C, D, A₁, B₁, C₁, D₁). То есть мы получили, что у прямоугольного параллелепипеда 8 вершин и 12 рёбер. Грани прямоугольного параллелепипеда, которые не имеют общих вершин, называют противолежащими (в нашем случае это пары: ABB₁A₁ и DCC₁D₁, ABCD и A₁B₁C₁D₁, ADD₁A₁ и ВСС₁В₁). Противолежащие грани параллелепипеда равны.

Измерения прямоугольного параллелепипеда - это длина трех рёбер, имеющих общую вершину. Например, ребра ВВ₁, В₁А₁, В₁С₁ являются измерениями ABCDA₁B₁C₁D₁:

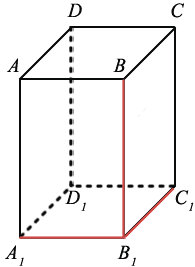
Измерения имеют названия: длина, ширина, высота. Данные названия введены, чтобы различать измерения:

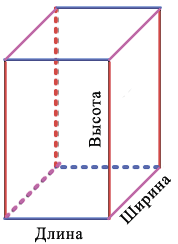
Диагональ параллелепипеда - это отрезок, соединяющий две его вершины, не принадлежащие одной грани. Например, AC₁ - диагональ ABCDA₁B₁C₁D₁:

Частным случаем прямоугольного параллелепипеда является куб. Куб - это прямоугольный параллелепипед, все измерения которого равны:

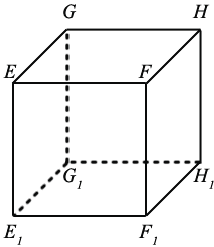
EFHGE₁F₁H₁G₁ - куб, его высота, ширина и длина равны. Гранями куба являются 6 равных квадратов.

Рассмотрим следующую фигуру:

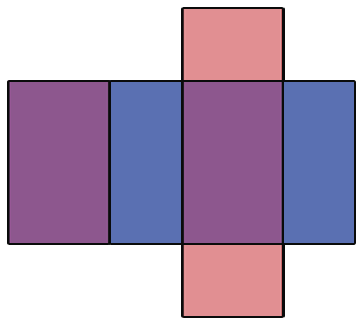
Данная фигура состоит из шести прямоугольников, которые попарно равны (выделены одним цветом). Если мы согнём по линиям данную фигуру и склеим, то получим модель прямоугольного параллелепипеда, противоположные грани которого будут одного цвета. Рассматриваемую фигуру называют развёрткой прямоугольного параллелепипеда. Как сказано выше, куб состоит из 6 равных квадратов, значит, его развертка будет иметь следующий вид:

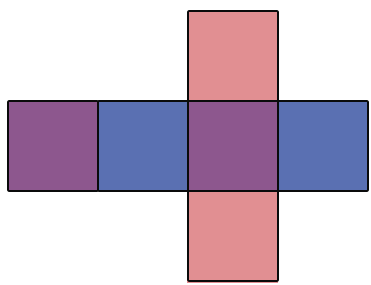
В данном случае куб "разрезали" по 6 горизонтальным ребрам и 1 вертикальному, при этом противоположные грани выделены одним цветом. Таким образом, "разрезая" любой многогранник по ребрам так, чтобы все грани оказались в одной плоскости, можно получить его развертку. Развертки многогранников нужны, например, для создания их объемных моделей.

Вторым многогранником, который мы рассмотрим, является пирамида. Пирамида - это многогранник, в основании которого лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину, которая является вершиной пирамиды.

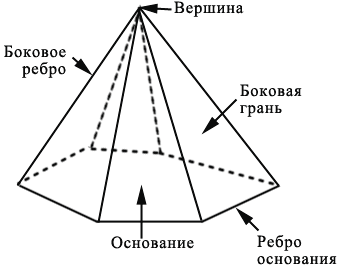
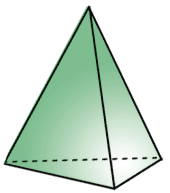
Рёбра основания пирамиды - это стороны основания пирамиды. Боковые рёбра пирамиды - это стороны боковых граней, которые не принадлежат основанию. Пирамида называется в соответствии с числом сторон многоугольника, который является его основанием. Например, на рисунке ниже изображены треугольная пирамида (тетраэдром) и пятиугольная пирамида.

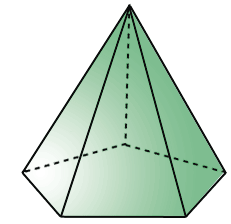
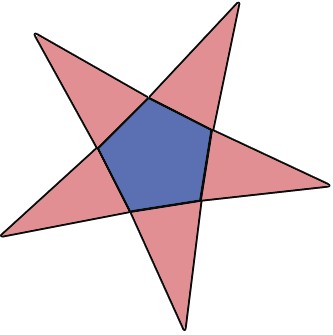
Если мы "разрежем" по боковым рёбрам пятиугольную пирамиду, то получим следующий многоугольник, который будет являться развёрткой данной пирамиды: