Упражнение 345 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 107

\( x^4 - 13x^2 + k = 0 \)

Пусть \( y = x^2 \quad (y \ge 0). \)

\(y^2 - 13y + k = 0\)

\[ D = 13^2 - 4\cdot1\cdot k = 169 - 4k. \]

а) Исходное уравнение имеет 4 корня, если \(D > 0\) у квадратного уравнения по \(y\) и его корни больше нуля:

\(169 - 4k > 0\)

\(-4k > -169\)   \(/ : (-4)\)

\( k < \frac{169}{4}\)

\( k < 42\frac{1}{4}\)

\(y_1 = \frac{13 + \sqrt D}{2} > 0\) при любом \(m\).

\(y_2 = \frac{13 - \sqrt D}{2} > 0\), если

\(13 - \sqrt D > 0\)

\(- \sqrt D > - 13\)  \(/\times (-1)\)

\(\sqrt D < 13\)

\((\sqrt D)^2 < 13^2\)

\(D < 169\)

\(169 - 4k < 169\)

\(-4k < 169 - 169\)

\(-4k < 0\)    \(/ : (-4)\)

\(k > 0\)

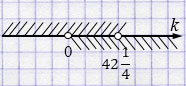
\(k \in (0; 42\frac14)\).

б) Исходное уравнение имеет 2 корня:

1) если \(D = 0\) у квадратного уравнения по \(y\) и его корень больше нуля.

\(169 - 4k = 0\)

\(-4k = - 169\)

\( k = \frac{169}{4}\)

\( k = 42\frac{1}{4}\)

\(y = \frac{13}{2}\)

\(y = 6,5 > 0\).

2) если \(D > 0\) у квадратного уравнения по \(y\) и один из его корней больше нуля, а другой меньше нуля.

\(169 - 4k > 0\)

\(-4k > -169\)   \(/ : (-4)\)

\( k < \frac{169}{4}\)

\( k < 42\frac{1}{4}\)

\(y_1 = \frac{13 + \sqrt D}{2} > 0\) при любом \(m\).

\(y_2 = \frac{13 - \sqrt D}{2} < 0\), если

\(13 - \sqrt D < 0\)

\(- \sqrt D < - 13\)  \(/\times (-1)\)

\(\sqrt D > 13\)

\((\sqrt D)^2 > 13^2\)

\(D > 169\)

\(169 - 4k > 169\)

\(-4k > 169 - 169\)

\(-4k > 0\)    \(/ : (-4)\)

\(k < 0\)

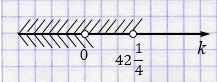
\(k \in (-\infty; 0)\).

в) Исходное уравнение не имеет корней, если \(D < 0\) у квадратного уравнения по \(y\). Случай, когда \(D > 0\) у квадратного уравнения по \(y\), а оба корня отрицательны, невозможен (смотри пункт а)).

\(169 - 4k < 0\)

\(-4k < -169\)   \(/ : (-4)\)

\( k > \frac{169}{4}\)

\( k > 42\frac{1}{4}\)

\(k \in \left(42\frac{1}{4}; +\infty\right)\).

Вывод:

а) уравнение имеет 4 корня при

\(k \in (0; 42\frac14)\).

б) уравнение имеет 2 корня при

\(k \in (-\infty; 0) \cup \{42\frac14\}\).

в) уравнение не имеет корней при

\(k \in \left(42\frac{1}{4}; +\infty\right)\).

Пояснения:

1. Подстановка \(y = x^2\) переводит биквадратное уравнение в обычное квадратное по \(y\).

2. Для подсчёта корней по \(x\) важно, что допустимы только корни \(y \ge 0\), и каждый положительный \(y\) даёт два корня \(x = \pm\sqrt{y}\), а \(y = 0\) даёт один корень \(x = 0\).

3. Так получаем полную классификацию числа корней исходного уравнения в зависимости от значения параметра \(k\).

Нужно отметить, что при \(k = 0\) уравнение \( x^4 - 13x^2 + k = 0 \) будет иметь 3 корня:

\( x^4 - 13x^2 = 0 \)

\(x^2(x^2 - 13) = 0\)

\(x^2 = 0\)  или  \(x^2 - 13 = 0\)

\(x = 0\)            \(x^2 = 13\)

                       \(x = \pm\sqrt{13}\).