Упражнение 350 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 108

а) \((3x - 5)(x + 4)(2 - x) = 0\)

или  \(3x - 5 = 0 \)

        \(3x = 5\)

        \(x = \frac{5}{3}\)

        \(x = 1\frac{2}{3}\)

или  \(x + 4 = 0 \)

        \(x = -4\)

или  \(2 - x = 0\)

        \(x = 2\)

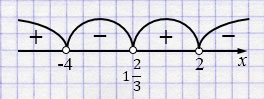
б) \((3x - 5)(x + 4)(2 - x) > 0\)

\(x \in (-\infty; -4) \cup \left(1\frac23; 2\right)\).

в) \((3x - 5)(x + 4)(2 - x) < 0\)

\(x \in \left(-4; 1\frac23\right) \cup (2; + \infty)\).

Ответ: а) при \(x = -4;\, 1\frac23;\, 2\);

б) при \(x \in (-\infty; -4) \cup \left(1\frac23; 2\right)\);

в) \(x \in \left(-4; 1\frac23\right) \cup (2; + \infty)\).

Пояснения:

Произведение двух выражений равно нулю, если нулю равен хотя бы один из множителей.

При решении неравенств используем метод интервалов.

Метод интервалов применяется к произведению вида \((x-a)(x-b)\dots\).

Находим нули каждого множителя — это точки, в которых знак выражения меняется.

Отмечаем точки на числовой прямой и определяем знак выражения на каждом интервале. Достаточно определить знак на одном интервале, а на остальных расставить знаки так, чтобы они чередовались. Чтобы определить знак на одном из интервалов, нужно взять какое-нибудь значение из рассматриваемого интервала и определить знак функции при этом значении.

Если знак требуется «>0» — берём интервалы со знаком "+", без корней; если «<0» — интервалы со знаком "–", без корней.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

У \(+\infty\) и \(-\infty\) при записи промежутка скобка всегда круглая.