Упражнение 344 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 107

а) \(x^4 - 12x^2 + c = 0\)

Пусть \(t = x^2 \ge 0\).

\( t^2 - 12t + c = 0 \)

\(D = (-12)^2 - 4\cdot1\cdot c =\)

\(= 144 - 4c\)

1) Если \(D < 0\), то уравнение не имеет корней.

\(144 - 4c < 0\)

\(-4c < -144\)   \(/ : (-4)\)

\(с > 36\)

2) Если \(D \ge 0\), то уравнение имеет корни, но они должны быть отрицательны.

\(144 - 4c \ge 0\)

\(-4c \ge -144\)   \(/ : (-4)\)

\(с \le 36\)

\(t_{1,2} = \frac{12\pm\sqrt D}{2} \)

\(y = \frac{12+\sqrt D}{2} > 0\), значит, исходное уравнение имеет не менее двух корней \(x = \pm\sqrt t\) при \(с \le 36\).

Ответ: \( c > 36. \)

б) \(x^4 + cx^2 + 100 = 0\)

Пусть \(t = x^2 \ge 0\).

\[ t^2 + ct + 100 = 0 \]

\(D = c^2 - 4\cdot1\cdot100 =\)

\(=c^2 - 400\).

1) Если \(D < 0\), то уравнение не имеет корней.

\(c^2 - 400 < 0\)

\(y = c^2 - 400\) - парабола, ветви которой направлены вверх.

\(с^2 - 400 = 0\)

\(c^2 = 400\)

\(c = \pm \sqrt{400}\)

\(c = \pm 20\)

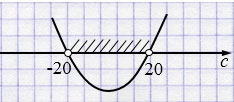
При \(c\in(-20; 20)\) исходное уравнение не имеет корней.

2) Если \(D \ge 0\), то уравнение имеет корни, но они должны быть отрицательны.

\(c^2 - 400 \ge 0\)

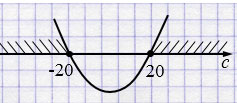
\(D \ge 0\) при \(c \in (-\infty; -20] \cup [20; +\infty)\).

\(t_{1,2} = \frac{-c \pm \sqrt D}{2a}\).

Оба корня будут отрицательны при

\(-c \pm \sqrt D < 0\).

Если \(c \in (-\infty; -20]\), то \(-c > 0\) и \(-c + \sqrt D > 0\), значит, исходное уравнение имеет не менее двух корней \(x = \pm\sqrt t\).

Если \(c \in [20; +\infty)\), то \(-c < 0\) и

\(-c + \sqrt D < 0\)

\(-c < -\sqrt D \)   \(/\times(-1)\)

\(c > \sqrt D\)

\(c^2 > D\)

\(c^2 > c^2 - 400\) - верно при любом \(c\), значит уравнение \( t^2 + ct + 100 = 0\) имеет два отрицательных корня, тогда уравнение \(x^2 = t\) не имеет корней.

При \(c \in [20; +\infty)\) исходное уравнение не имеет корней.

3) \((-20; 20) \cup [20; +\infty) = (-20; +\infty) \)

Ответ: \(c\in (-20; +\infty) \).

Пояснения:

1. Каждое биквадратное уравнение заменяется на квадратное по \(t = x^2\), и мы ищем, когда оно не имеет неотрицательных корней.

2. В пункте а) оказывается, что при наличии корней один из них обязательно будет ≥ 0, поэтому единственная возможность — отсутствие корней вообще, то есть \(D < 0\).

3. В пункте б) возможны два варианта: нет корней (что удовлетворяет условию), или оба корня отрицательные.