стр. 62 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник
Вернуться к содержанию учебника
Контрольные вопросы и задания
Вопрос
1. Сформулируйте определение квадратичной функции.
2. Как выглядит график квадратичной функции \(y = ax^2\) и какими свойствами обладает функция:
а) при \(a>0\);
б) при \(a<0\)?
3. Как из графика функции \(y = ax^2\) можно получить график функции:
а) \(y = ax^2 + n\);
б) \(y = a(x-m)^2\);
в) \(y = a(x-m)^2 + n\)?
4. Что представляет собой график квадратичной функции \(y = ax^2 + bx + c\)?
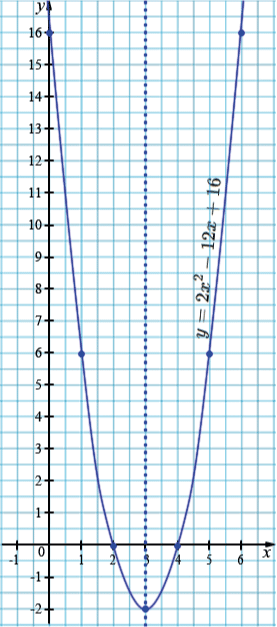
На примере функции \(y = 2x^2 - 12x + 16\) покажите, как строят график квадратичной функции.
Подсказка
Вспомните:
- Что такое функция, свойства функции.
- График функции.
- Квадратичную функцию и ее график.
- Степень с натуральным показателем.
- Сложение и вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Положение точек на координатной плоскости.
- Решение квадратных уравнений.
- Арифметический квадратный корень.
Ответ
1) Определение:
Квадратичной функцией называется функция, которую можно задать формулой вида
\(y=ax^2+bx+c,\)
где \(x\) - независимая переменная, \(a, b\) и \(c\) - некоторые числа, причём \(a\ne0.\)
2) Графиком функции \(y=ax^2\) является парабола, которая получается из параболы \(y=x^2\) растяжением от оси \(x\) в \(a\) раз, если \(a>1\), и сжатием к оси \(x\) в \(\frac1a\) раза, если \(0\lt a\lt 1\)
а) Свойства функции \(y=ax^2\) при \(a>0.\)
- Область определения функции - множество всех чисел, т.е. \(D(y)=(-\infty; +\infty).\)
- Если \(x=0\), то \(y=0\). График функции проходит через начало координат.
- Если \( x\ne0 \), то \(y>0\). График функции расположен в верхней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции; график функции симметричен относительно оси \(y.\) Функция является четной.
- Функция убывает на промежутке \( (-\infty; 0]\) и возрастает на промежутке \([0; +\infty)\).
- Наименьшее значение, равное нулю, функция принимает при \(x=0\), наибольшего значения функция не имеет.
- Множество значений функции - множество неотрицательных чисел, т.е. \(E(y)=[0; +\infty)\).
б) Свойства функции \(y=ax^2\) при \(a<0.\)
- Область определения функции - множество всех чисел, т.е. \(D(y)=(-\infty; +\infty).\)
- Если \(x=0\), то \(y=0\). График функции проходит через начало координат.
- Если \( x\ne0 \), то \(y<0\). График функции расположен в нижней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции; график функции симметричен относительно оси \(y.\) Функция является четной.
- Функция возрастает на промежутке \( (-\infty; 0]\) и убывает на промежутке \([0; +\infty)\).
- Наибольшее значение, равное нулю, функция принимает при \(x=0\), наименьшего значения функция не имеет.
- Множество значений функции - множество неположительных чисел, т.е. \(E(y)=(-\infty; 0]\).
3) а) График функции \(y=ax^2+n\) является параболой, которую можно получить из графика функции \(y=ax^2\) с помощью параллельного переноса вдоль оси \(y\) на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)
б) График функции \(y=a(x-m)^2\) является параболой, которую можно получить из графика функции \(y=ax^2\) с помощью параллельного переноса вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\).
в) График функции \(y=a(x-m)^2+n\) является параболой, которую можно получить из графика функции функции \(y=ax^2\) с помощью двух параллельных переносов: сдвига вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\), и сдвига вдоль оси \(y\) на на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)
4) Графиком функции \(y=ax^2+bx+c\) является парабола, которую можно получить из графика функции \(y=ax^2\) с помощью двух параллельных переносов - сдвига вдоль оси \(x\) и сдвига вдоль оси \(y.\) Вершиной данной параболы является точка \((m; n),\) где \(m=-\frac{b}{2a}\), \(n=-\frac{b^2-4ac}{4a.}\) Заметим, что ординату \(n\) можно находить, подставив найденное значение абсциссы в формулу \(y=ax^2+bx+c\). Осью симметрии параболы является прямая \(x=m,\) параллельная оси \(y.\) При \(a>0\) ветви параболы направленны вверх, а при \(a<0\) - вниз.
Пример:
\(y = 2x^2 - 12x + 16\).
1. Графиком данной функции является парабола, ветви которой направлены вверх \((a=2>0).\)
2. \(m=-\frac{b}{2a}=-\frac{-12}{2\cdot2}=3,\)
\(n = 2\cdot3^2 - 12\cdot3 + 16=-2\).
Вершина параболы: \((3; -2)\). Прямая \(x=3\) - ось симметрии параболы.
3. Нули функции:
\(2x^2 - 12x + 16=0\) \(|:2\)
\(x^2 - 6x + 8=0\)
\(D=b^2-4ac=(-6)^2-4\cdot1\cdot8=\)
\(=36-32=4,\) \(\sqrt{D}=2\)
\( x_{1,2} = \frac{-b \pm \sqrt{D}}{2a}\)
\( x_{1} = \frac{6+2}{2}=4\)
\( x_{2} = \frac{6-2}{2}=2\)
\((4; 0)\) и \((2; 0)\) - точка пересечения с осью \(x.\)
4. Точка пересечения с осью \(y:\)
\(x=0:\) \(y = 2\cdot0^2 - 12\cdot0 + 16=16\).
\((0; 16).\)
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(y\) | 16 | 6 | 0 | -2 | 0 | 6 | 16 |
Вернуться к содержанию учебника