стр. 43 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

1. Функцией называют такую зависимость переменной \(y\) от переменной \(x\), при которой каждому значению переменной \(x\) соответствует единственное значение переменной \(y\). Все значения зависимой переменной образуют область определения функции, а значения, которые принимает зависимая переменная, образуют множество значений функции. Область определения и множество значений функции \(y = f(x)\) обозначают соответственно \(D(f)\) и \(E(f)\).

2. Функция называется четной, если выполняются следующие условия:

- область определения функции симметрична относительно оси ординат (оси \(y\);

- противоположным значениям аргумента соответствуют равные значения функции.

Функция называется нечетной, если выполняются следующие условия:

- область определения функции симметрична относительно начала координат;

- противоположным значениям аргумента соответствуют противоположные значения функции.

Четная функция: \(y = x^2\).

Нечетная функция: \(y = x^3\).

Функция может не обладать ни свойством четности, ни свойством нечетности, например, функция \(y = 2x- 5\).

3. а) \(y = kx, k < 0\)

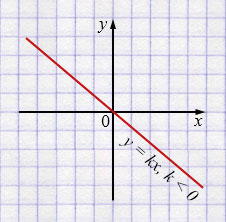
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x = 0\).

4. \(f(x) > 0\) при \(x < 0\),

\(f(x) < 0\) при \(x > 0\).

5. Убывает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений не имеет.

7. Функция нечетная.

б) \(y = kx + b, k > 0, b < 0\)

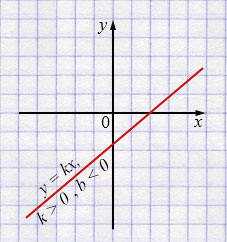
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x = -\frac{b}{k}\).

4. \(y > 0\) при \(x > -\frac{b}{k}\),

\(y < 0\) при \(x < -\frac{b}{k}\).

5. Функция возрастает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

в) \(y = \frac{k}{x}, k < 0\)

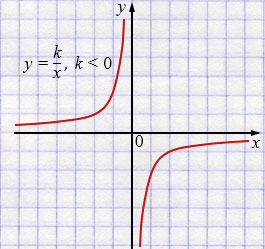
Свойства:

1. \(D(f) = (-\infty; 0) \cup (0; + \infty)\).

2. \(E(f) = (-\infty; 0) \cup (0; + \infty)\).

3. Нули функции не существуют.

4. \(y > 0\) при \(x < 0\),

\(y < 0\) при \(x > 0\).

5. Функция возрастает на \((-\infty; 0)\) и \((0; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция является нечетной.

г) \(y = x^2\)

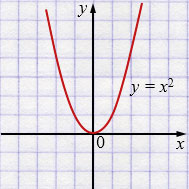
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = [0; +\infty)\).

3. \(y = 0\) при \(x = 0\).

4. \(y > 0\) при \(x \ne 0\).

5. Функция убывает на \((-\infty;0]\) и возрастает на \([0; + \infty)\).

6. Наименьшее значение функции равно нулю при \(x = 0\).

7. Функция является четной.

д) \(y = x^3\)

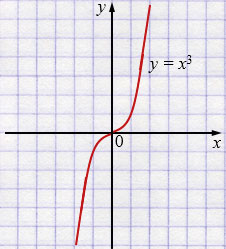
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x =0\).

4. \(y > 0\) при \(x > 0\),

\(y < 0\) при \(x < 0\).

5. Функция возрастает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция является нечетной.

е) \(y = \sqrt x\)

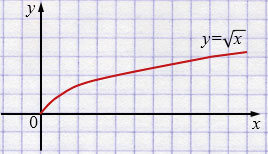
Свойства:

1. \(D(f) = [0; + \infty)\).

2. \(E(f) = [0; + \infty)\).

3. \(y = 0\) при \(x =0\).

4. \(y > 0\) при \(x > 0\).

5. Функция возрастает на \([0; + \infty)\).

6. Наименьшее значение функции равно нулю при \(x = 0\).

7. Функция не является ни четной и ни нечетной.

ж) \(y = |x|\)

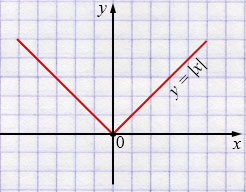
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = [0; +\infty)\).

3. \(y = 0\) при \(x = 0\).

4. \(y > 0\) при \(x \ne 0\).

5. Функция убывает на \((-\infty;0]\) и возрастает на \([0; + \infty)\).

6. Наименьшее значение функции равно нулю при \(x = 0\).

7. Функция является четной.