Упражнение 118 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 48

\(y=\frac14x^2\)

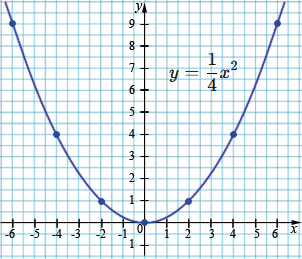
а) При \(x=-2,5\) \(y=1,5;\) 

при \(x= -1,5\) \(y=0,5;\) 

при \(x= 3,5\) \(y=3;\)

б) \(y=5\) при \(x=\pm4,5;\)

 \(y=3\) при \(x=\pm3,5;\)

\(y=2\) при \(x\approx\pm2,8;\)

в) Промежуток возрастания: \([0; +\infty )\).

Промежуток убывания функции: \((-\infty; 0]\).

Пояснения:

Функцией называют такую зависимость переменной \(y\) от переменной \(x\), при которой каждому значению переменной \(x\) соответствует единственное значение переменной \(y\).

Формула функции:

\( y=\frac14x^{2} \)

Это квадратичная функция вида \(y=ax^{2}\) с \(a>0\), значит график — парабола, направленная ветвями вверх. Строим график и по нему определяем значение функции при данном значении аргумента и наоборот, какому значению аргумента соответствует данное значение функции.

Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.