Упражнение 1054 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(\begin {cases} 6x(x - 1) - 3x(2x - 1) < x,\\[2pt]0,5x - 3,7 < 0,2x - 0,7\end {cases} \)

\(\begin {cases} \cancel{6x^2} - 6x - \cancel{6x^2} + 3x < x,\\[2pt] 0,5x - 0,2x < -0,7 + 3,7 \end {cases} \)

\(\begin {cases} - 6x + 3x + x < 0,\\[2pt] 0,3x < 3  / : 0,3 \end {cases} \)

\(\begin {cases} -2x < 0,   / : (-2) \\[2pt] 0,3x < 3  / : 0,3 \end {cases} \)

\(\begin {cases} x > 0, \\[2pt] x < 10 \end {cases} \)

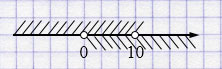
\(x \in (0; 10)\).

Ответ: \((0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10)\).

б) \(\begin {cases} 0{,}7x-3(0{,}2x+1)\le0{,}5x+1,\\[2pt]0{,}3(1-x)+0{,}8x\ge x+5{,}3\end {cases} \)

\(\begin {cases} 0{,}7x-0,6x-3\le0{,}5x+1,\\[2pt]0,3-0,3x+0{,}8x\ge x+5{,}3\end {cases} \)

\(\begin {cases} 0,1x-3\le0{,}5x+1,\\[2pt]0,3+0,5x\ge x+5{,}3\end {cases} \)

\(\begin {cases} 0,1x-0,5x\le1+3,\\[2pt]0,5x - x\ge 5{,}3 - 0,3\end {cases} \)

\(\begin {cases} -0,4x\le4,   / : (-0,4) \\[2pt]-0,5x\ge5  / : (-0,5)\end {cases} \)

\(\begin {cases} x\ge -10, \\[2pt] x\le -10 \end {cases} \)

Ответ: \(-10\).

в) \(\begin {cases} \tfrac13(3x-2)+\tfrac16(12x+1)>0,  /\times 6 \\[8pt]\tfrac17(14x-21)+\tfrac29(9x-6)<0  /\times 63 \end {cases} \)

\(\begin {cases} 2(3x-2)+(12x+1)>0,\\[8pt]9(14x-21)+14(9x-6)<0 \end {cases} \)

\(\begin {cases} 6x-4+12x+1>0,\\[8pt]126x-189+126x-84<0 \end {cases} \)

\(\begin {cases} 18x-3>0,\\[8pt]252x-273<0 \end {cases} \)

\(\begin {cases} 18x>3,  / : 18 \\[8pt]252x<273  / :252 \end {cases} \)

\(\begin {cases} x>\frac{3}{18}, \\[8pt] x<\frac{273}{252} \end {cases} \)

\(\begin {cases} x>\frac{1}{6}, \\[8pt] x<\frac{13}{12} \end {cases} \)

\(\begin {cases} x>\frac{1}{6}, \\[8pt] x<1\frac{1}{12} \end {cases} \)

\(x \in (\frac{1}{6}; 1\frac{1}{12})\)

Ответ: \(1\).

г) \(\begin {cases} 0,2(5x - 1) + \frac13(3x + 1) < x + 5,8,  /\times3 \\[2pt]8x - 7 - \frac16(6x - 2) > x /\times6\end {cases} \)

\(\begin {cases} 0,6(5x - 1) + (3x + 1) < 3x + 17,4, \\[2pt] 48x - 42 - (6x - 2) > 6x \end {cases} \)

\(\begin {cases} 3x - 0,6 + 3x + 1 < 3x + 17,4, \\[2pt] 48x - 42 - 6x + 2 > 6x \end {cases} \)

\(\begin {cases} 6x + 0,4 < 3x + 17,4, \\[2pt] 42x - 40 > 6x \end {cases} \)

\(\begin {cases} 6x - 3x < 17,4 - 0,4, \\[2pt] 42x - 6x > 40 \end {cases} \)

\(\begin {cases} 3x < 17,  / : 3 \\[2pt] 36x > 40  / : 36 \end {cases} \)

\(\begin {cases} x < \frac{17}{3}, \\[2pt] x > \frac{40}{36} \end {cases} \)

\(\begin {cases} x < 5\frac{2}{3}, \\[2pt] x > \frac{10}{9} \end {cases} \)

\(\begin {cases} x < 5\frac{2}{3}, \\[2pt] x > 1\frac19 \end {cases} \)

\(x \in (1\frac19; 5\frac23)\)

Ответ: \(2; 3; 4; 5\).

д) \(\begin {cases} \frac{z-1}{2}-\frac{z-4}{3} > 2z-1,  /\times6 \\[8pt]2z-\frac{z-5}{3}>0  / \times3 \end {cases} \)

\(\begin {cases}3(z-1)-2(z-4) > 12z-6, \\[8pt]6z-(z-5)>0 \end {cases} \)

\(\begin {cases}3z-3-2z+8 > 12z-6, \\[8pt]6z-z+5>0 \end {cases} \)

\(\begin {cases} z+5 > 12z-6, \\[8pt]5z+5>0 \end {cases} \)

\(\begin {cases} z-12z > -6-5, \\[8pt]5z>-5  / : 5 \end {cases} \)

\(\begin {cases} -11z > -11,  / : (-11) \\[8pt]z>-1 \end {cases} \)

\(\begin {cases} z < 1, \\[8pt]z>-1 \end {cases} \)

\(z \in(-1; 1)\).

Ответ: \(0\).

e) \(\begin {cases} 3y - \frac{1+5y}{4} < y,  /\times4 \\[8pt] \frac{4-y}{5} - y - 1 < 0  /\times5 \end {cases} \)

\(\begin {cases} 12y - (1+5y) < 4y, \\[8pt] 4-y - 5y - 5 < 0 \end {cases} \)

\(\begin {cases} 12y - 1-5y < 4y, \\[8pt] -6y - 1 < 0 \end {cases} \)

\(\begin {cases} 7y - 1 < 4y, \\[8pt] -6y < 1  / : (-6) \end {cases} \)

\(\begin {cases} 7y - 4y < 1, \\[8pt] y > -\frac16 \end {cases} \)

\(\begin {cases} 3y < 1,  / : 3 \\[8pt] y > -\frac16 \end {cases} \)

\(\begin {cases} y < \frac13, \\[8pt] y > -\frac16 \end {cases} \)

\(y \in (-\frac16; \frac13)\)

Ответ: \(0\).

Пояснения:

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Из общего промежутка выбираем целые значения.

При решении систем неравенств сначала раскрываем скобки, используя распределительное свойство умножения, затем используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку и точка не принадлежит промежутку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку и точка принадлежит промежутку.

а) от 18 до 23 лет: \(8\) рабочих;

от 43 до 48 лет: \(13\) рабочих.

б) Наибольшее число рабочих - возрастная группе от 33 до 38 лет: \(22\) рабочих.

в) Наименьшее число рабочих — возрастная группа от 53 до 58 лет: \(5\) - рабочих.

г) Общее число рабочих:

\( 8 + 14 + 20 + 22 + 17 + 13 + 12 + 5 = 111\)

Пояснения:

Гистограмма — это ступенчатая фигура, составленная из сомкнутых прямоугольников. Основание каждого прямоугольника равно длине интервала, а высота - частоте или относительной частоте. Таким образом, в гистограмме основания прямоугольников выбираются не произвольно, а строго определены длиной интервала.

Рассматриваемая гистограмма показывает количество рабочих в каждом возрастном интервале.

По горизонтальной оси отмечены интервалы шириной 5 лет: \([18;23], [23;28], [28;33], [33;38], [38;43], [43;48], [48;53], [53;58]\).

По вертикальной оси — частоты, которые поднимаются примерно до следующих значений: 8, 14, 20, 22, 17, 13, 12, 5.