Упражнение 1041 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1041 учебника 2023-2025 (стр. 230):
Решите неравенство:
а) \(\;\dfrac{x-0{,}5}{4}+\dfrac{x-0{,}25}{4}+\dfrac{x-0{,}125}{8}<0;\)
б) \(\;\dfrac{5-x}{3}-\dfrac{1-x}{2}>1.\)
№1041 учебника 2013-2022 (стр. 231):
Упростите выражение \(2\sqrt{5}(\sqrt{2}-\sqrt{5})-(\sqrt{5}+\sqrt{2})^2.\)
Подсказка
№1041 учебника 2023-2025 (стр. 230):
Вспомните:
- Решение неравенств с одной переменной.
- Числовые промежутки.
- Приведение дробей к общему знаменателю.
- Деление десятичных дробей.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Умножение обыкновенных дробей.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Распределительное свойство умножения.
- Подобные слагаемые.
№1041 учебника 2013-2022 (стр. 231):
Вспомните:
- Арифметический квадратный корень.
- Свойства арифметического квадратного корня.
- Распределительное свойство умножения.
- Квадрат суммы двух выражений.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№1041 учебника 2023-2025 (стр. 230):
а) \(\;\dfrac{x-0{,}5}{4}+\dfrac{x-0{,}25}{4}+\dfrac{x-0{,}125}{8}<0\) \(/\times8\)
\(2(x - 0,5) + 2(x - 0,25) + (x - 0,125) < 0\)
\(2x - 1 + 2x -0,5 + x - 0,125 < 0\)
\(5x - 1,625 < 0\)
\(5x < 1,625\) \( / : 5\)
\(x < 0,325\)

Ответ: \((-\infty; 0,325)\).
б) \(\;\dfrac{5-x}{3}-\dfrac{1-x}{2}>1\)\(/\times6\)
\(2(5-x) - 3(1-x) > 6\)
\(10 - 2x -3 + 3x > 6\)
\(7 + x > 6\)
\(x > 6 - 7\)
\(x > - 1\)
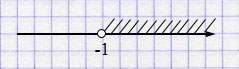
Ответ: \((-1; +\infty)\).
Пояснения:
Сначала в каждом неравенстве избавляемся от знаменателей, домножив неравенство на общий знаменатель дробей, входящих в неравенство, учитывая то, что если обе части неравенства умножить на одно и то же положительное число, то получится равносильное ему неравенство. Затем, используя распределительное свойство умножения, раскрываем скобки и приводим подобные слагаемые.
Затем при решении неравенств используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
№1041 учебника 2013-2022 (стр. 231):
\(2\sqrt{5}(\sqrt{2}-\sqrt{5})-(\sqrt{5}+\sqrt{2})^2=\)
\(=2\sqrt{5}\cdot\sqrt{2}-2\sqrt{5}\cdot\sqrt{5}-((\sqrt5)^2+2\sqrt5\cdot\sqrt2+(\sqrt2)^2)=\)
\(=2\sqrt{10} - 2\sqrt{25} - (5 + 2\sqrt{10} + 2) =\)
\(=\cancel{2\sqrt{10}} - 2\cdot5 - 5 - \cancel{2\sqrt{10}} - 2) =\)
\(=-10-5-2 = -17\).
Пояснения:
1. Раскрытие скобок выполняется по формуле:
\[ k(a-b)=ka-kb. \]
2. Квадрат суммы раскрывается по формуле:
\[ (a+b)^2 = a^2 + 2ab + b^2. \]
3. Умножение корней выполняем по правилу:
\[ \sqrt{a}\cdot \sqrt{b}=\sqrt{ab}. \]
Шаг за шагом раскрываем скобки, приводим подобные члены. Члены \(2\sqrt{10}\) в выражении взаимно уничтожились, осталось только числовое выражение.
Вернуться к содержанию учебника