Упражнение 478 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№478 учебника 2023-2025 (стр. 110):
Постройте график функции, заданной формулой:
а) \(y = \frac{\sqrt{x^2}}{x}\);
б) \(y = \frac{-2\sqrt{x^2}}{x}\);
в) \(y = x\sqrt{x^2}\);
г) \(y = -x\sqrt{x^2}\).
№478 учебника 2013-2022 (стр. 112):
Вычислите:
а) \(15\sqrt{20}\cdot0{,}1\sqrt{45}\);
б) \(0{,}3\sqrt{10}\cdot0{,}2\sqrt{15}\cdot0{,}5\sqrt{6}\);
в) \(\displaystyle \frac{8\sqrt{5}}{0{,}4\sqrt{0{,}2}}\);
г) \(\displaystyle \frac{\sqrt{0{,}48}}{5\sqrt{12}}\).
Подсказка
№478 учебника 2023-2025 (стр. 110):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Модуль числа.
- Область определения функции.
- Линейная функция, ее график.
- Квадратичная функция, ее график (парабола).
- Координаты точки.
№478 учебника 2013-2022 (стр. 112):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Умножение десятичных дробей.
- Свойства умножения.
- Деление десятичных дробей.
- Умножение обыкновенных дробей.
Ответ
№478 учебника 2023-2025 (стр. 110):
а) \(\displaystyle y=\frac{\sqrt{x^2}}{x}=\frac{|x|}{x}\), \(x\neq0\).
\(y=\begin{cases} 1,&x>0,\\ -1,&x<0. \end{cases}\)
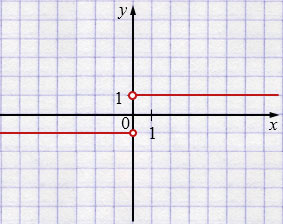
б) \(\displaystyle y=\frac{ -2\sqrt{x^2}}{x}=\frac{-2|x|}{x}\), \(x\neq0\).
\(y=\begin{cases} -2,&x>0,\\ 2,&x<0. \end{cases}\)
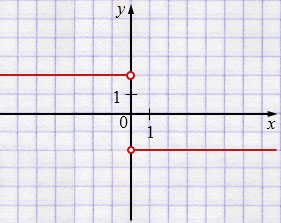
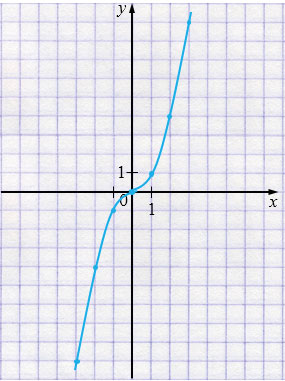
в) \(\displaystyle y=x\sqrt{x^2}=x\cdot|x|\)
\(y=\begin{cases} x^2,&x\ge0,\\ -\,x^2,&x<0. \end{cases}\)
\(y=x^2\), \(x \ge 0\)
| \(x\) | 0 | 1 | 2 | 3 |
| \(y\) | 0 | 1 | 4 | 9 |
\(y=-x^2\), \(x \le 0\)
| \(x\) | 0 | -1 | -2 | -3 |
| \(y\) | 0 | -1 | -4 | -9 |
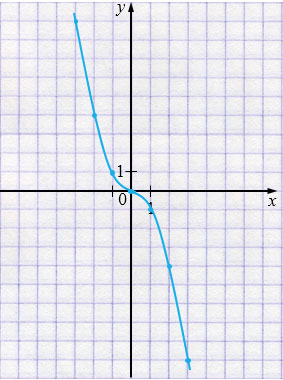
г) \(\displaystyle y=-x\sqrt{x^2}=-x\cdot|x|\)
\(y=\begin{cases} -\,x^2,&x\ge0,\\ x^2,&x<0. \end{cases}\)
\(y=-x^2\), \(x \ge 0\)
| \(x\) | 0 | 1 | 2 | 3 |
| \(y\) | 0 | -1 | -4 | -9 |
\(y=x^2\), \(x \le 0\)
| \(x\) | 0 | -1 | -2 | -3 |
| \(y\) | 0 | 1 | 4 | 9 |
Пояснения:
Основное правило:
\(\sqrt{x^2}=|x|\) для любого \(x\).
– Определение модуля:
\(|a| = a\), при \(a \ge 0\);
\(|a| = -a\), при \(a \le 0\).
– Функция \(y=\frac{|x|}{x}\) не существует при \(x=0\), так как на нуль делить нельзя, поэтому на графике точки с абсциссой \(x=0\) "выколотые" и график этой функции состоит из двух кусочков (лучей, параллельных оси \(x\)) \(x = 1\) при \(x \ge 0\) и \(y = -1\) при \(x<0\).
– Функция \(y=\frac{ -2|x|}{x}\) не существует при \(x=0\), так как на нуль делить нельзя, поэтому на графике точки с абсциссой \(x=0\) "выколотые" и график этой функции состоит из двух кусочков (лучей, параллельных оси \(x\)) \(y=-2\) при \(x \ge 0\) и \(y = 2\) при \(x<0\).
– Функция \(y = x\cdot|x|\) определена при всех значениях \(x\) (выколотых точек нет), графиком является кусочно-заданная парабола:
\(y=x^2\) для \(x\ge0\) и
\(y = -x^2\) для \(x<0\).
– Функция \(y = -x\cdot|x|\) определена при всех значениях \(x\) (выколотых точек нет), графиком является кусочно-заданная парабола:
\(y=-x^2\) для \(x\ge0\) и
\(y = x^2\) для \(x<0\).
№478 учебника 2013-2022 (стр. 112):
а) \(15\sqrt{20}\cdot0{,}1\sqrt{45} =\)
\(=15\cdot0{,}1\;\sqrt{20\cdot45} =\)
\(=1{,}5\sqrt{900} =1{,}5\cdot30 =45\).
б) \(0{,}3\sqrt{10}\cdot0{,}2\sqrt{15}\cdot0{,}5\sqrt{6} =\)
\(=(0{,}3\cdot0{,}2\cdot0{,}5)\;\sqrt{10\cdot15\cdot6} =\)
\(=0{,}03\sqrt{900} =0{,}03\cdot30 =0{,}9\).
в) \( \frac{8\sqrt{5}}{0{,}4\sqrt{0{,}2}} =\frac{8}{0{,}4}\cdot\sqrt{\frac{5}{0{,}2}} =\)
\(=\frac{80}{4}\cdot\sqrt{\frac{50}{2}} =20\sqrt{25} =\)
\(=20\cdot5 =100\).
г) \( \frac{\sqrt{0{,}48}}{5\sqrt{12}} =\frac15\cdot\sqrt{\frac{0,48}{12}}=\)
\(=0,2\cdot\sqrt{0,04}=0,2\cdot0,2 = 0,04\)
Пояснения:
Использованные приемы:
1) От перемены мест множителей произведение не изменяется.
2) Свойство корня из произведения:
\(\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}\).
3) Свойство корня из дроби:
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\).
4) Произведение дробей:
\(\frac{ab}{cd} = \frac{a}{c}\cdot\frac{b}{d}\).
Вернуться к содержанию учебника