Упражнение 621 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№621 учебника 2023-2025 (стр. 135):
Решите уравнение:

№621 учебника 2013-2022 (стр. 137):
Представьте в виде многочлена:
а) \(6x(x - 3) - x(2 - x);\)
б) \(-a^2(3a - 5) + 4a(a^2 - a);\)
в) \(ax(2x - 3a) - x\bigl(ax + 5a^2\bigr);\)
г) \(-4m^2\bigl(n^2 - m^2\bigr) + 3n^2\bigl(m^2 - n^2\bigr).\)
Подсказка
№621 учебника 2023-2025 (стр. 135):
Вспомните:
- Линейное уравнение.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
- Свойства уравнений.
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Сложение и вычитание десятичных дробей.
№621 учебника 2013-2022 (стр. 137):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Приведение подобных слагаемых.
- Свойства степени с натуральным показателем.
Ответ
№621 учебника 2023-2025 (стр. 135):
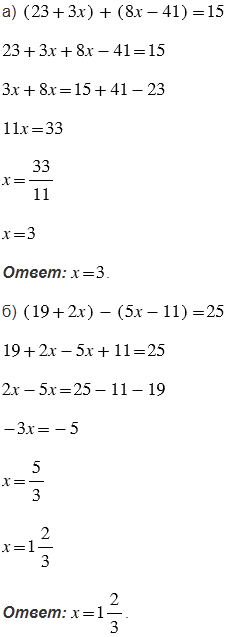



№621 учебника 2013-2022 (стр. 137):
а) \( 6x^2 - 18x - \bigl(2x - x^2\bigr) = \)
\( = 6x^2 - 18x - 2x + x^2 = \)
\( = 7x^2 - 20x. \)
б) \( -3a^3 + 5a^2 + 4a^3 - 4a^2 = \)
\( = ( -3a^3 + 4a^3 ) + (5a^2 - 4a^2) = \)
\( = a^3 + a^2. \)
в) \( 2ax^2 - 3a^2x - \bigl(a x^2 + 5a^2x\bigr) = \)
\( = 2ax^2 - 3a^2x - a x^2 - 5a^2x = \)
\( = (2ax^2 - a x^2) + (-3a^2x - 5a^2x) = \)
\( = ax^2 - 8a^2x. \)
г) \( -4m^2n^2 + 4m^4 + 3n^2m^2 - 3n^4 = \)
\( = 4m^4 + (-4m^2n^2 + 3m^2n^2) - 3n^4 = \)
\( = 4m^4 - m^2n^2 - 3n^4. \)
Пояснения:
• В каждой части применён распределительный закон: раскрытие скобок \(k(u\pm v)=ku\pm kv\).
• Затем выполнено сложение и вычитание подобных членов: объединены одночлены с одинаковыми буквенными частями.
• Итоговые выражения упорядочены по убыванию степеней по каждой переменной для наглядности.
Вернуться к содержанию учебника