Упражнение 619 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№619 учебника 2023-2025 (стр. 135):
Докажите, что значение выражения не зависит от значения переменной:
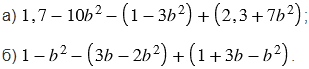
№619 учебника 2013-2022 (стр. 136):
Представьте в виде многочлена:
а) \(14b + 1 - 6(2 - 11b);\)
б) \(25(2 - 3c) + 16(5c - 1);\)
в) \(14(7x - 1) - 7(14x + 1);\)
г) \(36(2 - y) - 6(5 - 2y).\)
Подсказка
№619 учебника 2023-2025 (стр. 135):
Вспомните:
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Сложение и вычитание десятичных дробей.
№619 учебника 2013-2022 (стр. 136):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Приведение подобных слагаемых.
Ответ
№619 учебника 2023-2025 (стр. 135):

Пояснения:
Выражение не зависит от переменной, если в ходе преобразований получается выражение, не содержащее эту переменную.
При выполнении преобразований сначала раскрываем скобки, учитывая знаки, стоящие перед ними (знак "минус" перед скобками меняет знаки слагаемых в скобках при раскрытии на противоположные), далее приводим подобные слагаемые (в решении выделены одинаковым цветом). Подобные слагаемые, которые в сумме дают ноль, вычеркнуты.
№619 учебника 2013-2022 (стр. 136):
а) \( 14b + 1 - 6(2 - 11b) = \)
\( =14b + 1 - 12 + 66b = \)
\( = (14b + 66b) + (1 - 12) = \)
\( = 80b - 11. \)
б) \( 25(2 - 3c) + 16(5c - 1) = \)
\( = 50 - 75c + 80c - 16 = \)
\( = ( -75c + 80c) + (50 - 16) = 5c + 34. \)
в) \( 14(7x - 1) - 7(14x + 1) = \)
\( = 98x - 14 - 98x - 7 = \)
\( = (98x - 98x) + (-14 - 7) = -21. \)
г) \( 36(2 - y) - 6(5 - 2y) = \)
\( 72 - 36y - 30 + 12y = \)
\( = (72 - 30) + (-36y + 12y) = \)
\( = 42 - 24y. \)
Пояснения:
• Сначала применили распределительный закон: умножили каждый член скобок на коэффициент перед ними.
\(k(u+v)=ku+kv\).
• Затем сложили полученные одночлены, объединив подобные (с одинаковыми буквенными частями).
• В конце записали результат в виде упрощённого многочлена.
Вернуться к содержанию учебника