Упражнение 617 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№617 учебника 2023-2025 (стр. 134):
Какой двучлен нужно сложить с многочленом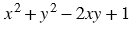 
, чтобы в результате получился многочлен:
а) не содержащий переменную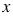 
;
б) не содержащий переменную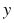 
?
№617 учебника 2013-2022 (стр. 136):
Выполните умножение:
а) \(-3x^2(-x^3 + x - 5)\);
б) \((1 + 2a - a^2)\cdot5a\);
в) \(\tfrac{2}{3}x^2y\,(15x - 0{,}9y + 6)\);
г) \(3a^4x\,(a^2 - 2ax + x^3 - 1)\);
д) \((x^2y - xy + xy^2 + y^3)\cdot3xy^2\);
е) \(-\tfrac{3}{7}a^4\,(2{,}1b^2 - 0{,}7a + 35)\).
Подсказка
№617 учебника 2023-2025 (стр. 134):
Вспомните:
- Многочлены.
- Сложение и вычитание многочленов.
- Раскрытие скобок, подобные слагаемые.
- Противоположные числа.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№617 учебника 2013-2022 (стр. 136):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Умножение рациональных чисел.
- Десятичная запись дробных чисел.
- Умножение обыкновенных дробей.
- Сокращение обыкновенных дробей.
- Свойства степени с натуральным показателем.
Ответ
№617 учебника 2023-2025 (стр. 134):
№617 учебника 2013-2022 (стр. 136):
а) \( -3x^2(-x^3 + x - 5) = \)
\( =3x^5 - 3x^3 + 15x^2. \)
б) \( (1 + 2a - a^2)\cdot5a = \)
\( = 5a +10a^2 - 5a^3. \)
в) \( \tfrac{2}{3}x^2y(15x - 0{,}9y + 6) = \)
\( =10x^3y - 0{,}6x^2y^2 + 4x^2y. \)
г) \( 3a^4x(a^2 - 2ax + x^3 - 1) = \)
\( = 3a^6x - 6a^5x^2 + 3a^4x^4 - 3a^4x \)
д) \( (x^2y - xy + xy^2 + y^3)\cdot3xy^2 = \)
\( = 3x^3y^3 - 3x^2y^3 + 3x^2y^4 + 3xy^5. \)
е) \( -\tfrac{3}{7}a^4(2{,}1b^2 - 0{,}7a + 35) = \)
\( = - 0{,}9a^4b^2 + 0{,}3a^5 - 15a^4. \)
Пояснения:
Применён распределительный закон: множитель вне скобок умножается на каждый член внутри скобок.
\( X(Y+Z)=XY+XZ \).
Коэффициенты (дробные и десятичные) умножаются отдельно, затем записываются показатели степеней переменных.
Вернуться к содержанию учебника