Упражнение 616 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№616 учебника 2023-2025 (стр. 134):
(Для работы в парах.) Учащимся была предложена задача: "Найдите значение выражения
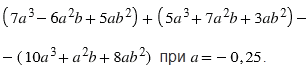
Один из учеников сказал, что в задаче не хватает данных. Прав ли он?
1) Обсудите друг с другом, в каком случае ученик окажется прав.
2) Выполните преобразования.
3) Сделайте вывод.
№616 учебника 2013-2022 (стр. 136):
Представьте в виде многочлена:
а) \(\frac{2}{7}x\,(1{,}4x^2 - 3{,}5y);\)
б) \(-\frac{1}{3}c^2\,(1{,}2d^2 - 6c);\)
в) \(\frac{1}{2}ab\bigl(\frac{2}{3}a^2 - \frac{3}{4}ab + \frac{4}{5}b^2\bigr);\)
г) \(-\frac{2}{5}a^2y^5\bigl(5ay^2 - \frac{1}{2}a^2y - \frac{5}{6}a^3\bigr).\)
Подсказка
№616 учебника 2023-2025 (стр. 134):
Вспомните:
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Степень с натуральным показателем.
- Десятичная запись дробных чисел.
- Умножение обыкновенных дробей.
- Сокращение дробей.
- Умножение рациональных чисел.
№616 учебника 2013-2022 (стр. 136):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Умножение рациональных чисел.
- Десятичная запись дробных чисел.
- Умножение обыкновенных дробей.
- Сокращение обыкновенных дробей.
- Свойства степени с натуральным показателем.
Ответ
№616 учебника 2023-2025 (стр. 134):


№616 учебника 2013-2022 (стр. 136):
а) \( \frac{2}{7}x(1{,}4x^2 - 3{,}5y) = \)
\( =\frac{2\cdot1{,}4}{7}x^3 -\frac{2\cdot3{,}5}{7}xy =\)
\(= 0{,}4x^3 - xy.\)
б) \(-\frac{1}{3}c^2(1{,}2d^2 - 6c) = \)
\( = -0{,}4c^2d^2 + 2c^3. \)
в) \( \frac{1}{2}ab\Bigl(\frac{2}{3}a^2 - \frac{3}{4}ab + \frac{4}{5}b^2\Bigr) = \)
\( =\frac{1}{3}a^3b - \frac{3}{8}a^2b^2 + \frac{2}{5}ab^3. \)
г) \( -\frac{2}{5}a^2y^5\bigl(5ay^2 - \frac{1}{2}a^2y - \frac{5}{6}a^3\bigr) = \)
\( = -2a^3y^7 + \frac{1}{5}a^4y^6 + \frac{1}{3}a^5y^5. \)
Пояснения:
В каждом пункте применён распределительный закон: множитель вне скобок умножается на каждый член внутри скобок.
\( X(Y+Z)=XY+XZ \).
Десятичные коэффициенты и дроби умножаются отдельно, затем знак и степени переменных записываются вместе с коэффициентом.
Полученные одночлены упорядочены по убыванию степеней (для наглядности), объединений подобныx членов не требуется.
Вернуться к содержанию учебника