Задание 2.387 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№2.387 учебника 2023-2024 (стр. 96):
Подсчитайте на своих моделях число граней, вершин, ребер у треугольной пирамиды; у четырехугольной пирамиды. А сколько граней, вершин, ребер у семиугольной пирамиды?
№2.387 учебника 2021-2022 (стр. 91):
Упростите выражение:
Подсказка
№2.387 учебника 2023-2024 (стр. 96):
Вспомните, что называют пирамидой, ее элементы.
№2.387 учебника 2021-2022 (стр. 91):
Вспомните:
- Распределительное свойство умножения.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Основное свойство дроби.
- Свойства сложения.
- Свойства вычитания.
Ответ
№2.387 учебника 2023-2024 (стр. 96):
У треугольной пирамиды:
4 грани, 4 вершины и 6 ребер.
У четырехугольной пирамиды:
5 граней, 5 вершин и 8 ребер.
У семиугольной пирамиды:
8 граней, 8 вершин и 14 ребер.
Пояснения:
У любой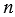 
- угольной пирамиды:
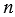( + 1) граней,
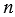( + 1) вершин;
2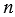 ребер.
№2.387 учебника 2021-2022 (стр. 91):
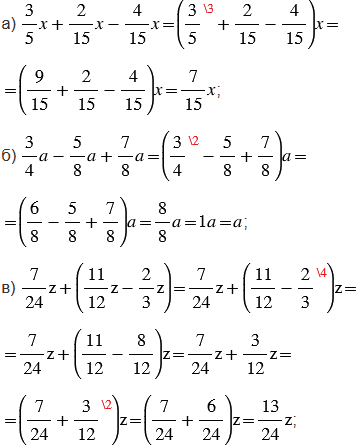
Пояснения:
Чтобы упростить данные выражения, используем распределительное свойство умножения относительно сложения или относительно вычитаем, а именно выносим одинаковый множитель (букву) за скобки и выполняем вычисления в скобках по правилам, указанным ниже.
Чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним.
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо: привести данные дроби к общему знаменателю, а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Если при вычислениях получилась сократимая дробь ее нужно сократить. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Вернуться к содержанию учебника