Задание 2.392 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.392 учебника 2023-2024 (стр. 97):
В субботу Катя прочитала  всей книги, причем до обеда она прочитала
всей книги, причем до обеда она прочитала 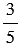 прочитанного за субботу. Какую часть книги прочитала Катя до обеда в субботу?
прочитанного за субботу. Какую часть книги прочитала Катя до обеда в субботу?
№2.392 учебника 2021-2022 (стр. 91):
Маршрут равен  км. В первый день туристы прошли
км. В первый день туристы прошли 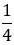 маршрута. Какую часть маршрута осталось пройти? Найдите значение получившегося выражения при
маршрута. Какую часть маршрута осталось пройти? Найдите значение получившегося выражения при  = 56;
= 56;  = 232;
= 232;  =
= 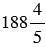 .
.
Подсказка
№2.392 учебника 2023-2024 (стр. 97):
Вспомните:
- Как найти часть от числа, умножение обыкновенных дробей.
- Сокращение дробей.
№2.392 учебника 2021-2022 (стр. 91):
Вспомните:
- Числовые и буквенные выражения.
- Как найти часть от числа, умножение обыкновенных дробей.
- Распределительное свойство умножения.
- Неправильные дроби.
- Вычитание дробей с одинаковыми знаменателями.
- Сокращение дробей.
- Деление и дроби.
Ответ
№2.392 учебника 2023-2024 (стр. 97):

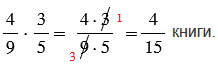
Ответ: 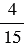 прочитала Катя до обеда в субботу.
прочитала Катя до обеда в субботу.
Пояснения:
Чтобы найти дробь от числа (десятичную или обыкновенную), нужно умножить число на эту дробь.
В субботу Катя прочитала 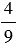 всей книги, причем до обеда она прочитала
всей книги, причем до обеда она прочитала 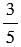 прочитанного за субботу. Значит, Катя прочитала до обеда в субботу:
прочитанного за субботу. Значит, Катя прочитала до обеда в субботу:
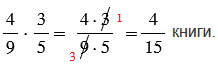
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на их наибольший общий делитель.
№2.392 учебника 2021-2022 (стр. 91):
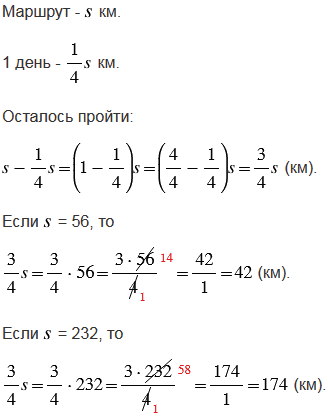
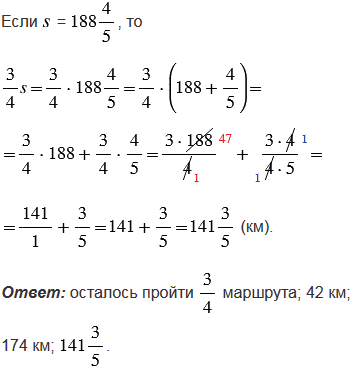
Пояснения:
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Маршрут равен 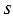 км. В первый день туристы прошли
км. В первый день туристы прошли 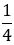 маршрута, значит, в первый день туристы прошли
маршрута, значит, в первый день туристы прошли 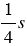 км. Следовательно, туристам осталось пройти:
км. Следовательно, туристам осталось пройти:
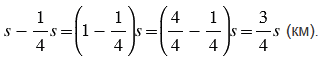
Чтобы упростить выражение, мы использовали распределительное свойство умножения относительно вычитания, а именно вынесли общий множитель 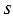 за скобки и выполнили вычисления в скобках, учитывая то, что единицу можно представить в виде неправильной дроби с одинаковыми числителем и знаменателем и, чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
за скобки и выполнили вычисления в скобках, учитывая то, что единицу можно представить в виде неправильной дроби с одинаковыми числителем и знаменателем и, чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Чтобы найти значение буквенного выражения при заданном значении переменной, нужно в это выражение вместо буквы подставить, соответствующие ей, числа и выполнить вычисления.
Получается, чтобы найти значение буквенного выражения 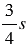 , нужно в это выражение вместо буквы
, нужно в это выражение вместо буквы 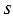 подставить, соответствующие ей, числа и выполнить вычисления (смотри решение).
подставить, соответствующие ей, числа и выполнить вычисления (смотри решение).
Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на их наибольший общий делитель. Также помним, дробь, у которой в знаменателе стоит единица, равна своему числителю.
Чтобы умножить смешанное число на обыкновенную дробь, используем распределительное свойство умножения, а именно, чтобы умножить смешанное число на обыкновенную дробь, можно:
1) умножить целую часть на обыкновенную дробь;
2) умножить дробную часть на эту обыкновенную дробь;
3) сложить полученные результаты.
Вернуться к содержанию учебника