Задание 2.130 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.130 учебника 2023-2024 (стр. 62):
а) Каким должен быть знаменатель обыкновенной дроби, чтобы ее можно было представить в виде десятичной?
б) Какие дроби можно представить в виде десятичной дроби:
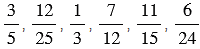 ?
?
№2.130 учебника 2021-2022 (стр. 52):
Турист плыл на байдарке 1,5 ч со скоростью 6,6 км/ч и 3,5 ч шел пешком со скоростью 5,4 км/ч. Найдите среднюю скорость туриста.
Подсказка
№2.130 учебника 2023-2024 (стр. 62):
Вспомните:
- Обыкновенные дроби.
- Десятичные дроби.
- Разложение на простые множители.
- Какие числа называют простыми.
- Основное свойство дроби.
- Наибольший общий делитель.
№2.130 учебника 2021-2022 (стр. 52):
Вспомните:
- Как найти среднюю скорость.
- Задачи на движение.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение десятичных дробей.
Ответ
№2.130 учебника 2023-2024 (стр. 62):
а) Чтобы обыкновенную дробь можно было представить в виде десятичной дроби, ее знаменатель при разложении на простые множители не должен содержать простых множителей отличных от 2 и 5.

Пояснения:
а) Чтобы обыкновенную дробь можно было представить в виде десятичной дроби, ее знаменатель при разложении на простые множители не должен содержать простых множителей отличных от 2 и 5, так как только из множителей 2 и 5, используя основное свойство дроби, мы можем получить дробь, у которой в знаменателе стоит единица с нулями (десятичную дробь), а затем записать эту дробь с помощью запятой.
б) Чтобы понять можно ли дробь представить в виде десятичной дроби, нужно разложить ее знаменатель на простые множители (смотри пункт а)), при этом обязательно проверяем, чтобы дробь была несократимая, если дробь сократимая, то ее сначала сокращаем, а затем знаменатель сокращенной дроби раскладываем на простые множители.
Сократить дробь, значит, разделить числитель и знаменатель дроби на их наибольший общий делитель.
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Если из двух чисел большее число делится на меньшее, то наибольшим общим делителем этих двух чисел будет меньшее число чисел.
№2.130 учебника 2021-2022 (стр. 52):
1) 6,6 • 1,5 = 9,9 (км) - турист проплыл на байдарке.
| × | 6 | 6 | |
| 1 | 5 | ||
| + | 3 | 3 | 0 |
| 6 | 6 | ||
| 9 | 9 | 0 |
2) 5,4 • 3,5 = 18,9 (км) - турист прошел пешком.
| × | 5 | 4 | ||
| 3 | 5 | |||
| + | 2 | 7 | 0 | |
| 1 | 6 | 2 | ||
| 1 | 8 | 9 | 0 |
3) 9,9 + 18,9 = 28,8 (км) - общее расстояние, которое преодолел турист.
| + | 1 | 8 | , | 9 |
| 9 | , | 9 | ||
| 2 | 8 | , | 8 |
4) 1,5 + 3,5 = 5 (ч) - общее время в пути.
5) 28,8 : 5 = 5,76 (км/ч).
| - | 2 | 8 | 8 | 5 | ||||||||||||
| 2 | 5 | 5 | 7 | 6 | ||||||||||||
| - | 3 | 8 | ||||||||||||||
| 3 | 5 | |||||||||||||||
| - | 3 | 0 | ||||||||||||||
| 3 | 0 | |||||||||||||||
| 0 |
Ответ: средняя скорость туриста равна 5,76 км/ч.
Пояснения:
Чтобы найти среднюю скорость движения, нужно весь пройденный путь разделить на все время движения.
Чтобы найти расстояние нужно скорость умножить на время.
Турист плыл на байдарке 1,5 ч со скоростью 6,6 км/ч, значит, на байдарке турист проплыл:
6,6 • 1,5 = 9,9 (км).
Турист 3,5 ч шел пешком со скоростью 5,4 км/ч, значит, пешком турист прошел:
5,4 • 3,5 = 18,9 (км).
Получается общее расстояние, которое преодолел турист:
9,9 + 18,9 = 28,8 (км).
На байдарке турист плыл 1,5 ч, шел пешком - 3,5 ч, значит, общее время в пути:
1,5 + 3,5 = 5 (ч).
Итак, турист всего преодолел 28,8 км за 5 ч, значит, средняя скорость туриста:
28,8 : 5 = 5,76 (км/ч).
Вернуться к содержанию учебника