Задание 691 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№691 учебника 2013-2022 (стр. 182):
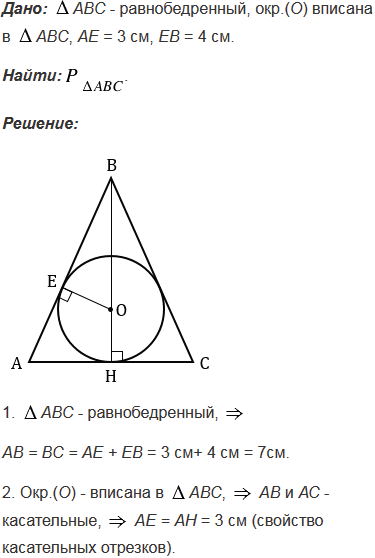
Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.
№691 учебника 2023-2024 (стр. 180):
Начертите отрезок АВ и разделите его в отношении: а) 2 : 5; б) 3 : 7; в) 4 : 3.
Подсказка
№691 учебника 2013-2022 (стр. 182):
Вспомните:
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое биссектриса, медиана треугольника.
- Какая окружность называется вписанной.
- Что такое периметр треугольника.
- Свойство касательных отрезков.
- Свойство биссектрисы угла.
№691 учебника 2023-2024 (стр. 180):
Вспомните:
- Что такое отрезок.
- Как построить отрезок, равный данному.
- Что такое луч.
- Что такое прямая.
- Какие прямые называются параллельными.
- Признаки параллельности двух прямых.
- Что такое окружность.
- Что такое отношение отрезков.
- Как построить угол, равный данному.
Ответ
№691 учебника 2013-2022 (стр. 182):



№691 учебника 2023-2024 (стр. 180):
а) Дано: отрезок АВ.
Разделить АВ в отношении 2 : 5.
Решение:
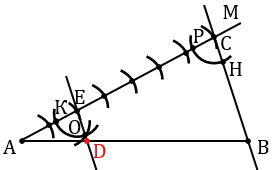
АD : DВ = 2 : 5.
б) Дано: отрезок АВ.
Разделить АВ в отношении 3 : 7.
Решение:
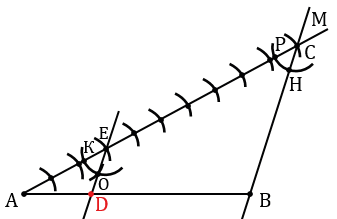
АD : DВ = 3 : 7.
в) Дано: отрезок АВ.
Разделить АВ в отношении 4 : 3.
Решение:
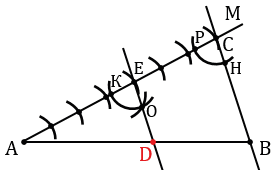
АD : DВ = 4 : 3.
Пояснения:
Чертим отрезок АВ и проводим какой-нибудь луч АМ, не лежащий на прямой АВ.
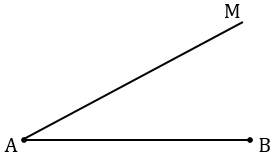
Далее на АМ откладываем последовательно 7 равных отрезков (т.к. нам нужно разделить отрезок АВ в отношении 2 : 5, а 2 + 5 =7). Для этого с помощью циркуля строим последовательно 7 окружностей одинакового радиуса, при этом центр первой окружности лежит в точке А, а центр каждой последующей в точке пересечения предыдущей окружности с лучом АМ (полностью окружности строить необязательно, смотри выделенное красным цветом). Точку пересечения последней окружности с лучом АМ обозначаем буквой С, проводим прямую через точки В и С.
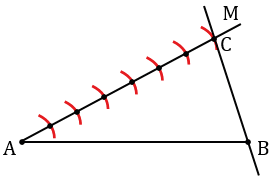
Обозначим точку пересечения второй окружности и луча АМ буквой Е и построим прямую ЕК параллельную прямой ВС. Для этого строим окружность произвольного радиуса с центром в точке С (полностью окружность строить необязательно, смотри выделенное синим цветом), точки пересечения данной окружности с лучом АМ и прямой ВС обозначаем буквами Р и Н соответственно.
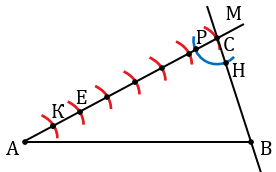
Затем строим окружность радиуса СН с центром в точке Е (всю окружность строить необязательно, смотри выделенное зеленым цветом), точку пересечения данной окружности с лучом АМ обозначаем буквой К. Измеряем с помощью циркуля расстояние РН и строим окружность с центром в точке К радиуса РН (всю окружность строить необязательно, смотри выделенное фиолетовым цветом цветом). Точку пересечения окружностей с центрами в точке Е и К обозначаем буквой О.
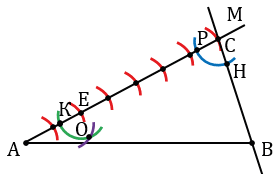
Далее проводим прямую через точки Е и О. Точку пересечения прямой ЕО с отрезком АВ обозначаем буквой D. Прямая ЕD параллельна прямой ВС по признаку параллельности двух прямых (соответственные углы АСВ и АЕD равны по построению). Точка D делит отрезок АВ в отношении 2 : 5, то есть АD : DВ = 2 : 5 (доказательство данного утверждения мы проводили ранее).

б) Все построения делаем аналогично пункту а).
в) Все построения делаем аналогично пункту а).
Вернуться к содержанию учебника