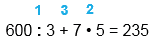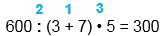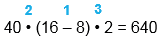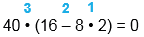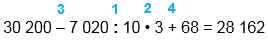Страница 16 - ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
61. Реши задачи, сравни решения.
1) Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч, а второй - со скоростью 14 км/ч. Найди расстояние между посёлками.
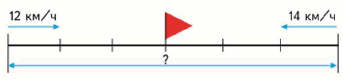
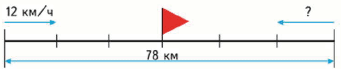
2) Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, а второй - со скоростью 14 км/ч. Через сколько часов лыжники встретились?
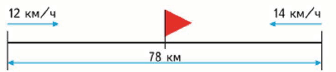
3) Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Решение
Задача 1:
1) 12 • 3 = 36 (км) - прошёл первый лыжник.
2) 14 • 3 = 42 (км) - прошёл второй лыжник.
3) 36 + 42 = 78 (км)
Ответ: расстояние между посёлками - 78 км.
Задача 2:
1) 12 + 14 = 26 (км/ч) - скорость сближения.
2) 78 : 26 = 3 (ч)
Ответ: через 3 ч встретились лыжники.
Задача 3:
1) 78 : 3 = 26 (км/ч) - скорость сближения.
2) 26 - 12 = 14 (км/ч)
Ответ: скорость второго лыжника - 14 км/ч.
В первом случае мы искали расстояние между поселками, умножив скорость на время каждого из лыжников и сложив результаты. Во втором - нашли скорость сближения и разделив расстояние между поселками на скорость сближения. А в третьем - нашли скорость сближения и вычли из неё скорость первого лыжника.
Пояснение
Чтобы найти скорость, нужно расстояние разделить на время.
Чтобы найти время, нужно расстояние разделить на скорость.
Скорость сближения - это сумма двух скоростей, с которой пешеходы приближаются друг к другу.
Вопрос
62. Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Решение
Задача 1:
Два пешехода вышли одновременно навстречу друг другу из двух посёлков и встретились через 2 ч. Первый пешеход шёл со скоростью 4 км/ч, а второй - со скоростью 5 км/ч. Найди расстояние между посёлками.
1) 4 • 2 = 8 (км) - прошёл первый пешеход.
2) 5 • 2 = 10 (км) - прошёл второй пешеход.
3) 8 + 10 = 18 (км)
Ответ: расстояние между посёлками - 18 км.
Задача 2:
Из двух посёлков, расстояние между которыми 18 км, вышли одновременно навстречу друг другу два пешехода. Первый из них шёл со скоростью 4 км/ч, а второй - со скоростью 5 км/ч. Через сколько часов пешеходы встретились?
1) 4 + 5 = 9 (км/ч) - скорость сближения.
2) 18 : 9 = 2 (ч)
Ответ: пешеходы встретились через 2 ч.
Задача 3:
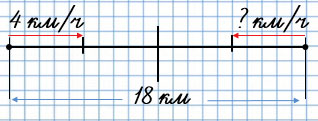
Из двух посёлков, находящихся на расстоянии 18 км, вышли одновременно навстречу друг другу два пешехода и встретились через 2 ч. Первый пешеход шёл со скоростью 4 км/ч. С какой скоростью шёл второй пешеход?
1) 18 : 2 = 9 (км/ч) - скорость сближения.
2) 9 - 4 = 5 (км/ч)
Ответ: скорость второго пешехода - 5 км/ч.
Пояснение
1)
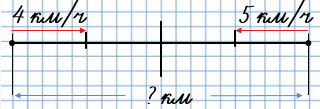
Чтобы найти расстояние, нужно скорость умножить на время.
2)
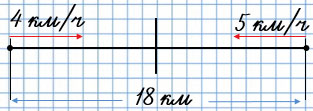
Чтобы найти время, нужно расстояние разделить на скорость.
Скорость сближения - это сумма двух скоростей, с которой пешеходы приближаются друг к другу.
3)
Чтобы найти скорость, нужно расстояние разделить на время.
Вопрос
63. (Устно.)
| 600 : 3 + 7 • 5 | 40 • (16 - 8) • 2 |
| 600 : (3 + 7) • 5 | 40 • (16 - 8 • 2) |
Ответ
Решение
600 : 3 + 7 • 5 = 235
600 : (3 + 7) • 5 = 300
40 • (16 - 8) • 2 = 640
40 • (16 - 8 • 2) = 0
Пояснение
|
1) 600 : 3 = 200 2) 7 • 5 = 35 3) 200 + 35 = 235 |
|
1) 3 + 7 = 10 2) 600 : 10 = 60 3) 60 • 5 = 300 |
|
1) 16 - 8 = 8 2) 40 • 8 = 320 3) 320 • 2 = 640 |
|
1) 8 • 2 = 16 2) 16 - 16 = 0 3) 40 • 0 = 0 |
Вопрос
64. 8 070 • 600
5 010 - 15 900 : 100 + 786
Подсказка
Ответ
Решение

5 010 - 15 900 : 100 + 786 = 5 637
Пояснение
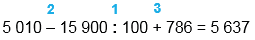
1) 15 900 : 100 = 159
| • | • | • | |||
| 2) | - | 5 | 0 | 1 | 0 |
| 1 | 5 | 9 | |||
| 4 | 8 | 5 | 1 |
| 3) | + | 4 | 8 | 5 | 1 |
| 7 | 8 | 6 | |||
| 5 | 6 | 3 | 7 |
Выполняем действия в выражении 8 070 • 600 по алгоритму умножения трёхзначного числа на однозначное, не обращая внимания на нули, а затем приписываем в произведении то количество нулей, которое было в конце множителей.
Вопрос
9 800 • 30
30 200 - 7 020 : 10 • 3 + 68
Подсказка
Ответ
Вопрос
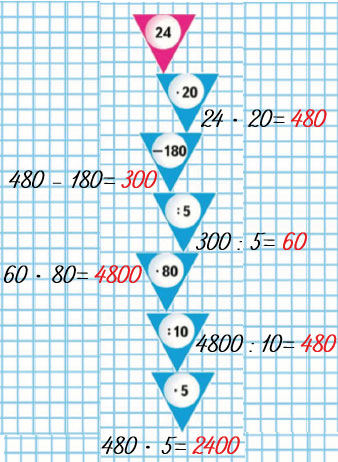
Цепочка
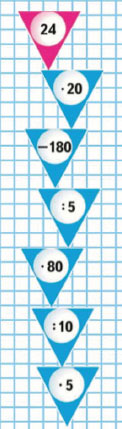
Вернуться к содержанию учебника