Страница 11 - ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
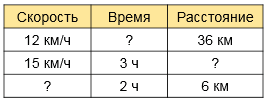
3. Составь задачи, используя данные таблицы, и реши их.
Подсказка
Взаимосвязь между скоростью, временем и расстоянием.
Ответ
Решение
Велосипедист проехал 36 км со скоростью 12 км/ч. За какое время он преодолел это расстояние?
36 : 12 = 3 (ч)
Ответ: за 3 ч.
Катер плыл со скоростью 15 км/ч на протяжении 3 ч. Какой путь прошёл катер?
15 • 3 = 45 (км)
Ответ: 45 км прошёл катер.
Пешеход прошёл 6 км за 2 ч. С какой скоростью он шёл?
6 : 2 = 3 (км/ч)
Ответ: 3 км/ч - скорость пешехода.
Пояснение
Чтобы найти время, нужно расстояние разделить на скорость.
Чтобы найти расстояние, нужно скорость умножить на время.
Чтобы найти скорость, нужно расстояние разделить на время.
Вопрос
4. Одновременно навстречу друг другу вышли два поезда: из Москвы - товарный, а из Санкт-Петербурга - пассажирский. Скорость пассажирского поезда была в 2 раза больше, чем скорость товарного. На каком расстоянии от Москвы встретятся поезда, если считать, что расстояние между этими городами 660 км?
Подсказка
Повтори, что такое доли.
Ответ
Решение
1) 1 + 2 = 3 (ч.) - всего.
2) 660 : 3 = 220 (км)
Ответ: на расстоянии 220 км от Москвы.
Пояснение
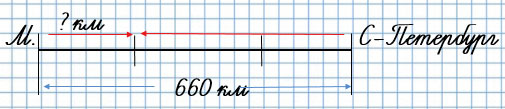
Пусть товарный поезд прошёл 1 часть пути, тогда пассажирский поезд - в 2 раза больше, то есть 2 части пути. Узнаем, сколько частей составляет весь путь:
1) 1 + 2 = 3 (ч.)
Весь путь - 3 части, это 660 км. Узнаем, чему равна 1 часть пути, которая и будет равна расстоянию от Москвы до места встречи поездов:
2) 660 : 3 = 220 (км)
Вернуться к содержанию учебника