Задание 155 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 48
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№155 учебника 2013-2022 (стр. 48):
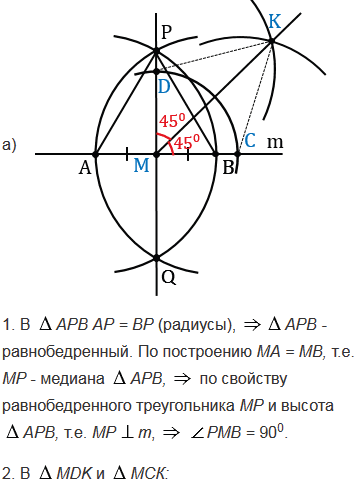
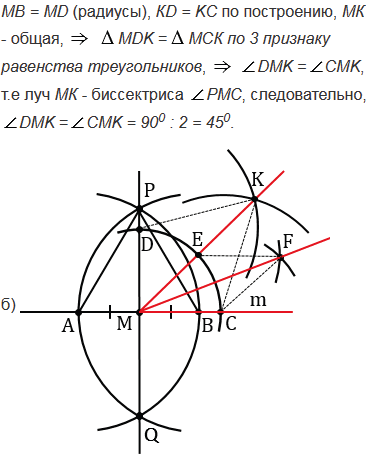
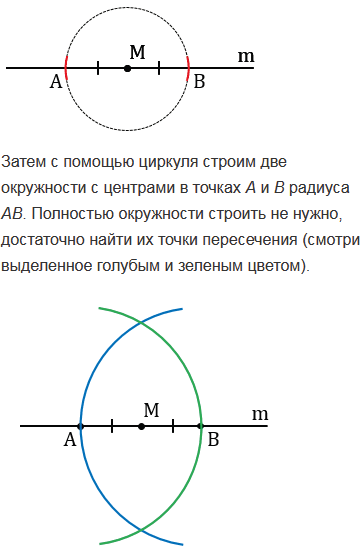
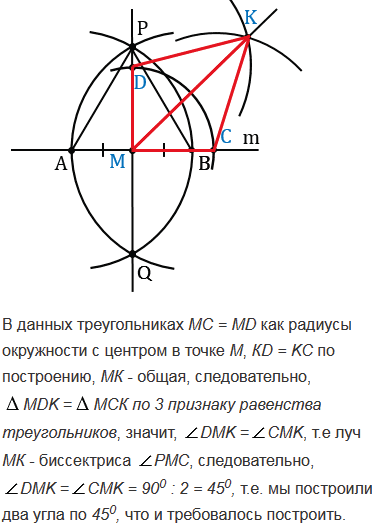
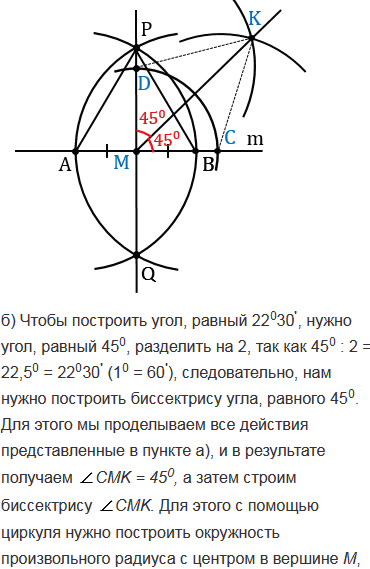
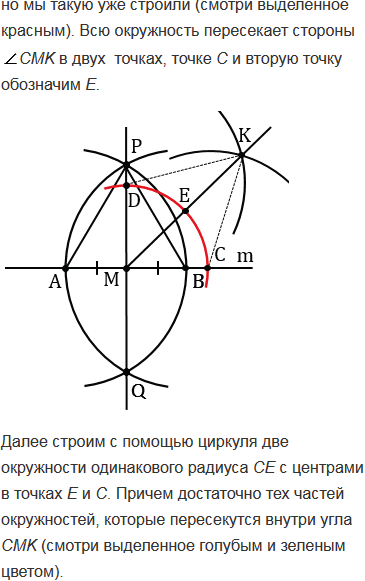
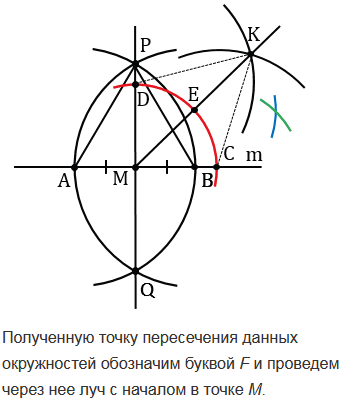
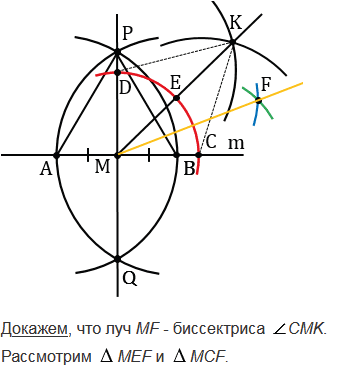
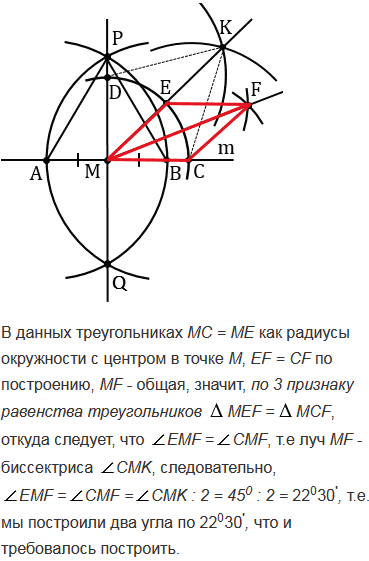
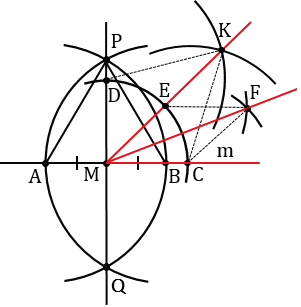
С помощью циркуля и линейки постройте угол, равный: а) 450; б) 22030'.
№155 учебника 2023-2024 (стр. 48):
Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окружности так, чтобы АМ = PQ. Всегда ли задача имеет решение?
Подсказка
№155 учебника 2013-2022 (стр. 48):
Вспомните:
- Как построить перпендикулярные прямые.
- Как построить биссектрису угла.
- Третий признак равенства треугольников.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое медиана треугольника.
- Что такое биссектриса треугольника.
- Что такое высота треугольника.
№155 учебника 2023-2024 (стр. 48):
Вспомните:
- Что такое окружность и ее характеристики.
- Что называется отрезком.
- Как построить отрезок, равный данному.
Ответ
№155 учебника 2013-2022 (стр. 48):


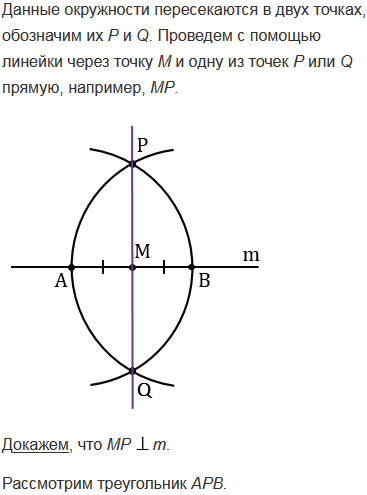
№155 учебника 2023-2024 (стр. 48):
1 случай
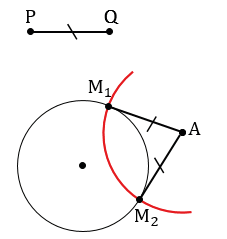
АМ1 =PQ, АМ2 = PQ.
Ответ: 2 решения.
2 случай
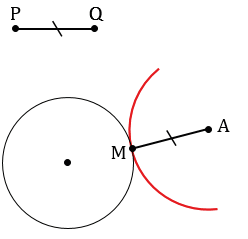
АМ = PQ.
Ответ: 1 решение.
3 случай
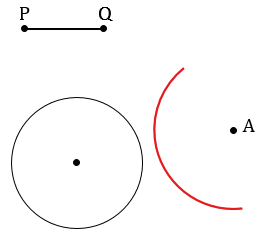
Ответ: нет решений.
Пояснения:
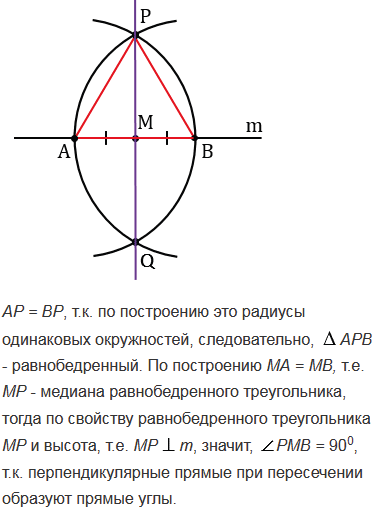
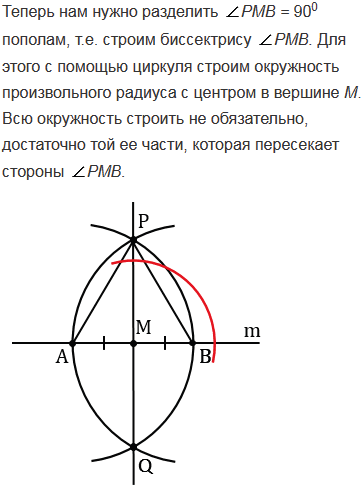
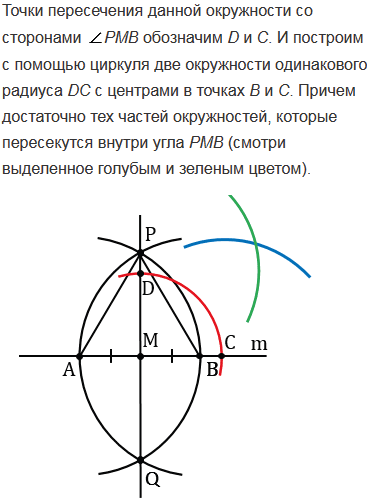
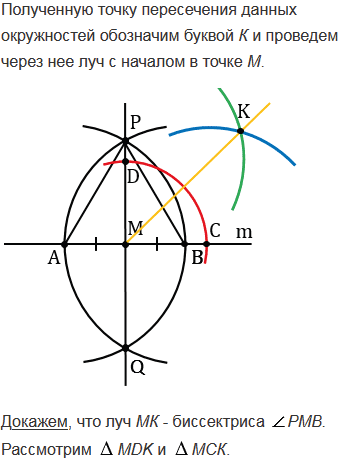
Решение данной задачи сводится к тому, что нам нужно построить отрезок АМ, равный отрезку PQ. Т.е. нужно построить окружность радиуса PQ с центром в точке А и найти точку (точки) пересечения этой окружности с окружностью данной в условии задачи. Расстояние от точки А до точки (точек) пересечения двух окружностей будет равно PQ (т.к. все точки окружности располагаются от ее центра на одном и том же расстоянии, равном ее радиусу), значит, полученная точка (точки) пересечения и будет являться искомой точкой (точками) М. Возможны три случая решения данной задачи, все зависит от того, как расположены точка А и окружность данная в условии задачи друг относительно друга.
1 случай
С помощью линейки строим произвольный отрезок PQ и с помощью циркуля строим окружность произвольного радиуса. Отмечаем точку А, не лежащую на окружности данной в условии задачи так, что расстояние от точки А до данной окружности меньше длины отрезка PQ.
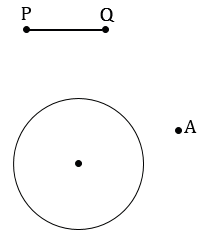
Далее с помощью циркуля измеряем отрезок PQ и строим часть окружности (смотри выделенное красным) радиуса PQ с центром в точке А. В данном случае можно не строить всю окружность целиком, так как нам важна только та часть, которая может иметь точки пересечения с данной окружностью.
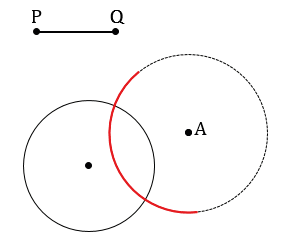
Получаем, что окружности пересекаются в двух точках, обозначим их М1 и М2.
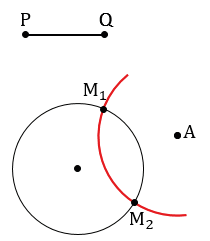
Каждая из этих точек будет находится на расстоянии PQ от точки А, так как АМ1 и АМ2 радиусы данной окружности, а все радиусы окружности равны, т.е. АМ1 = РQ, АМ2 = РQ, следовательно, задача в данном случае будет иметь два решения.

2 случай
С помощью линейки строим произвольный отрезок PQ и с помощью циркуля строим окружность произвольного радиуса. Отмечаем точку А, не лежащую на окружности данной в условии задачи так, что расстояние от точки А до данной окружности равно длине отрезка PQ.
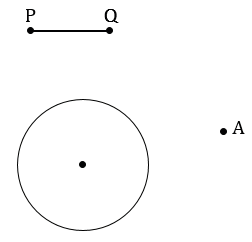
Далее с помощью циркуля измеряем отрезок PQ и строим часть окружности (смотри выделенное красным) радиуса PQ с центром в точке А. В данном случае можно не строить всю окружность целиком, так как нам важна только та часть, которая может иметь точки пересечения с данной окружностью.
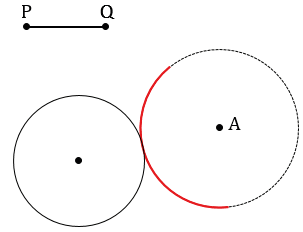
Получаем, что окружности пересекаются в одной точке, обозначим ее М.
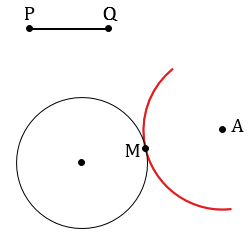
Точка М будет находится на расстоянии PQ от точки А, так как АМ1 радиус данной окружности, а все радиусы окружности равны, т.е. АМ = РQ, следовательно, задача в данном случае будет иметь одно решение.

3 случай
С помощью линейки строим произвольный отрезок PQ и с помощью циркуля строим окружность произвольного радиуса. Отмечаем точку А, не лежащую на окружности данной в условии задачи так, что расстояние от точки А до данной окружности больше длины отрезка PQ.
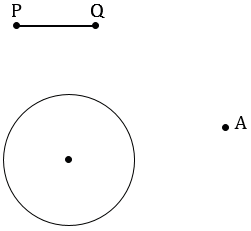
Далее с помощью циркуля измеряем отрезок PQ и строим часть окружности (смотри выделенное красным) радиуса PQ с центром в точке А. В данном случае можно не строить всю окружность целиком, так как нам важна только та часть, которая может иметь точки пересечения с данной окружностью.

Получаем, что точек пересечения окружности не имеют, т.е. в данном случае невозможно построить отрезок АМ такой, что АМ = PQ, учитывая то, что точка М должна лежать на окружности данной в условии задачи, значит решений нет.
Вернуться к содержанию учебника