Задание 2.362 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.362 учебника 2023-2024 (стр. 92):
Практическая работа
Оборудование: карандаш, линейка, транспортир, плотная бумага, ножницы, клей.
а) Задание: склейте модель треугольной пирамиды (рис. 2.8, а)
Порядок работы:
1) На плотном листе бумаги постройте развертку треугольной пирамиды по следующему алгоритму:
- Постройте равносторонний треугольник, используя алгоритм задачи 1,136, с. 34. Сторону треугольника возьмите больше 12 см, но меньше 20 см.
- Разделите каждую сторону треугольника пополам и соедините точки деления отрезками.
2) Нарисуйте клапаны (рис. 2,9, а).
3) Склейте модель треугольной пирамиды.
б) Задание: сделайте модель четырехугольной пирамиды (рис. 2.8, б).
Порядок работы:
1) На плотном листе бумаги постройте развертку четырехугольной пирамиды по следующему алгоритму:
- Постройте квадрат, сторона которого больше 6 см, но меньше 10 см.
- На сторонах квадрата постройте одинаковые равнобедренные треугольники, используя алгоритм задачи 1,136, с. 34. (сторона квадрата - основание равнобедренного треугольника). Боковую сторону треугольника возьмите больше 8 см, но меньше 16 см.
2) Нарисуйте клапаны (рис. 2,9, б).
3) Склейте модель четырехугольной пирамиды.
№2.362 учебника 2021-2022 (стр. 87):
Найдите какие-нибудь четыре решения неравенства:
а) 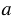 < 0,5;
< 0,5;
б) 5 < 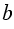 < 8;
< 8;
в) 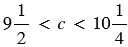 .
.
Подсказка
№2.362 учебника 2023-2024 (стр. 92):
Вспомните:
- Что называют пирамидой.
- Треугольник, виды треугольников.
№2.362 учебника 2021-2022 (стр. 87):
Вспомните:
- Сравнение десятичных дробей.
- Десятичная запись дробных чисел.
- Основное свойство дроби.
Ответ
№2.362 учебника 2023-2024 (стр. 92):
Практическую работу выполните самостоятельно.
№2.362 учебника 2021-2022 (стр. 87):
а) 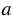 < 0,5
< 0,5
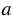 = 0; 0,1; 0,3; 0,4.
= 0; 0,1; 0,3; 0,4.
б) 5 < 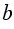 < 8
< 8
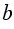 = 5,7; 6; 6,3; 7,5.
= 5,7; 6; 6,3; 7,5.
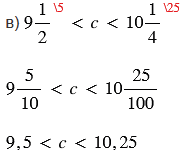
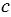 = 9,6; 9,9; 10; 10,1.
= 9,6; 9,9; 10; 10,1.
Пояснения:
Чтобы найти решения неравенств учитываем следующие правила:
1) из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше;
2) из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение).
3) любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.
Чтобы найти решения неравенства из пункта в), сначала преобразуем смешанные числа в десятичные дроби, используя основное свойство дроби, то есть умножаем числитель и знаменатель дробных частей смешанных чисел на такой дополнительный множитель, чтобы в знаменателе получилась единица с нулями, затем записываем полученные числа с помощью запятой, учитывая то, что целая часть смешанного числа, это целая часть десятичной дроби (записывается слева до запятой), а количество знаков после запятой совпадает с количеством нулей в знаменателе дробной части.
Вернуться к содержанию учебника