Задание 5. Применяем математику - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 140
Старая и новая редакции
Вернуться к содержанию учебника
Применяем математику. Страница 140
Вопрос
№5 учебника 2021-2022 (стр. 140):
При перевозке сена использовали грузовик, у которого длина кузова 4,4 м, ширина 2,3 м и высота 0,7 м. Грузоподъемность машины позволяла перевозить сена в два с четвертью раза больше. После увеличения высоты бортов объем кузова стал в два с четвертью раза больше. Вычислите высоту надстроенного кузова.
Подсказка
№5 учебника 2021-2022 (стр. 140):
Вспомните:
- Что называют прямоугольным параллелепипедом, как найти его объем.
- Умножение десятичных дробей.
- Обыкновенные дроби.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
Ответ
№5 учебника 2021-2022 (стр. 140):
1) 4,4 • 2,3 • 0,7 = 7,084 (м3) - объем грузовика.
|
|
2) 7,084 •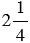 
= 7,084 • 2,25 =
= 15,939 (м3) - увеличенный объем грузовика.
| × | 7 | 0 | 8 | 4 | |||
| 2 | 2 | 5 | |||||
| + | 3 | 5 | 4 | 2 | 0 | ||
| 1 | 4 | 1 | 6 | 8 | |||
| 1 | 4 | 1 | 6 | 8 | |||
| 1 | 5 | 9 | 3 | 9 | 0 | 0 |
3) 15,939 : (4,4 • 2,3) = 15,939 : 10,12 =
= 1593,9 : 1012 = 1,575 (м) - новая высота.
| - | 1 | 5 | 9 | 3 | 9 | 1 | 0 | 1 | 2 | ||||||||||
| 1 | 0 | 1 | 2 | 1 | 5 | 7 | 5 | ||||||||||||
| - | 5 | 8 | 1 | 9 | |||||||||||||||
| 5 | 0 | 6 | 0 | ||||||||||||||||
| - | 7 | 5 | 9 | 0 | |||||||||||||||
| 7 | 0 | 8 | 4 | ||||||||||||||||
| - | 5 | 0 | 6 | 0 | |||||||||||||||
| 5 | 0 | 6 | 0 | ||||||||||||||||
| 0 |
Ответ: высота надстроенного кузова равна 1,575 м.
Пояснения:
Кузов грузовика имеет форму прямоугольного параллелепипеда. Объем прямоугольного параллелепипеда равен произведению трех его измерений (длины, ширины и высоты). Тогда объем кузова, у которого длина 4,4 м, ширина 2,3 м и высота 0,7 м, равен:
4,4 • 2,3 • 0,7 = 7,084 (м3).
После увеличения высоты бортов объем кузова стал в два с четвертью, то есть в 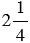, раза больше. Значит, объем увеличенного кузова равен:
7,084 • 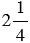= 7,084 • 2,25 = 15,939 (м3).
При вычислениях мы учли то, что четверть можно записать десятичной дробью 0,25, поэтому два с четвертью можно записать десятичной дробью 2,25
Чтобы найти одно из измерений прямоугольного параллелепипеда, нужно его объем разделить на произведение двух других его измерений.
При увеличении кузова грузовика изменили высоту, а длина и ширина остались неизменными, а именно 4,4 м и 2,3 м, тогда, учитывая то, что объем увеличенного кузова 15,939 м3, его высота будет равна:
5,939 : (4,4 • 2,3) = 15,939 : 10,12 =
= 1593,9 : 1012 = 1,575 (м).
Правила, по которым выполнены вычисления, смотрите в подсказке.
Вернуться к содержанию учебника