Упражнение 458 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 134
Вернуться к содержанию учебника
Вопрос
Постройте график уравнения:
а) \(x^2 - y^2 = 0\);
б) \(\dfrac{x^2 - y}{x} = 0\).
Подсказка
Ответ
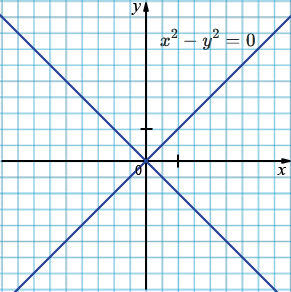
а) \(x^2 - y^2 = 0\)
\((x - y)(x+y) = 0\)
\((x - y)=0\) или \((x+y) = 0\)
\(y = x\) \(y = -x.\)
| \(x\) | 1 | -1 | \(x\) | -1 | 1 |
| \(y\) | 1 | -1 | \(y\) | 1 | -1 |
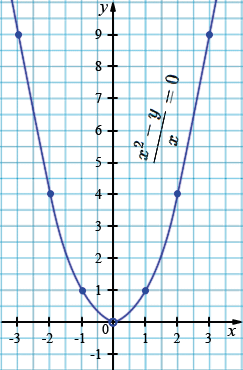
б) \(\frac{x^2 - y}{x} = 0\)
\(x \ne 0\)
\(x^2 - y = 0\)
\(y = x^2\)
Графиком данной функции является парабола, ветви которой направлены вверх, с выколотой точкой \((0; 0).\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Пояснения:
а) Уравнение \(x^2 - y^2 = 0\) можно разложить как разность квадратов:
\(x^2 - y^2 = (x - y)(x + y).\)
\((x - y)(x + y)=0.\)
Произведение равно нулю, значит один из множителей равен нулю:
\(x - y = 0\) или \(x + y = 0\)
\(y = x\) \(y = -x.\)
Следовательно, график состоит из двух пересекающихся прямых: \(y = x\) и \(y = -x\).
б) Дано уравнение:
\[\frac{x^2 - y}{x} = 0.\]
Дробь равна нулю, когда числитель равен нулю (при ненулевом знаменателе):
\[x^2 - y = 0.\]
Получаем:
\[y = x^2.\]
Это график параболы, ветви которой направлены вверх. Ограничение: \(x \ne 0\), но точка \((0;0)\) всё равно лежит на параболе. Однако в исходном выражении подстановка \(x=0\) невозможна, поэтому точка \((0;0)\) исключается.
График — парабола \(y = x^2\), с выколотой точкой \((0,0)\).
Вернуться к содержанию учебника