Упражнение 457 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 134

а) \(xy \ge 0\) 

Ответ: I и III координатные четверти , включая оси координат.

б) \(xy < 0\) 

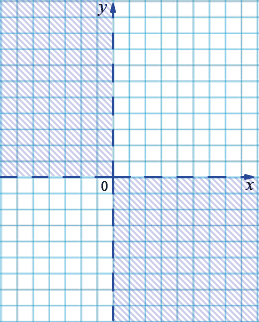
Ответ: II и IV координатные четверти, не включая оси координат.

Пояснения:

1. Знак произведения двух чисел зависит от их знаков:

- \(xy > 0\) — числа одного знака (оба положительные или оба отрицательные);

- \(xy < 0\) — числа разных знаков;

- \(xy = 0\) — хотя бы одно из чисел равно нулю.

Пояснение к пункту а)

Условие \(xy \ge 0\) включает случаи \(xy > 0\) и \(xy = 0\). Поэтому берём:

- оба положительные (I четверть),

- оба отрицательные (III четверть),

- любые точки на осях, где либо \(x = 0\), либо \(y = 0\).

Оси координат входят в решение, так как произведение равно нулю, а ноль удовлетворяет \(\ge 0\).

Пояснение к пункту б)

Условие \(xy < 0\) исключает случай равенства нулю и оставляет только противоположные знаки:

- \(x > 0\), \(y < 0\) (IV четверть),

- \(x < 0\), \(y > 0\) (II четверть).

Оси координат в решение не входят, потому что там произведение равно нулю, а ноль не меньше нуля.