Упражнение 449 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 133
Вернуться к содержанию учебника
Вопрос
Изобразите на координатной плоскости множество точек, заданное неравенством:
а) \(y \ge x\);
б) \(y \le x - 1\);
в) \(y > \frac14 x - 1\);
г) \(y < \frac13 x - 3\).
Подсказка
Вспомните:
- Что является решением неравенства с двумя переменными.
- Сложение и вычитание рациональных чисел.
- График линейной функции.
Ответ
а) \(y \ge x\);
\(y = x\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | 2 |
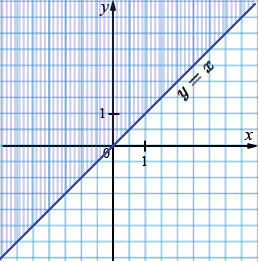
б) \(y \le x - 1\);
\(y = x - 1\)
| \(x\) | 0 | 1 |
| \(y\) | -1 | 0 |
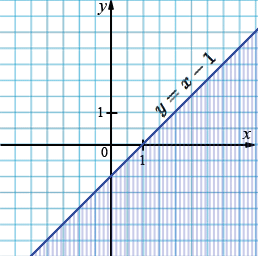
в) \(y > \frac14 x - 1\);
\(y = \frac14 x - 1\)
| \(x\) | 4 | -4 |
| \(y\) | 0 | -2 |
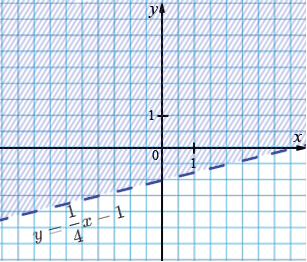
г) \(y < \frac13 x - 3\).
\(y = \frac13 x - 3\).
| \(x\) | 3 | 0 |
| \(y\) | -2 | -3 |
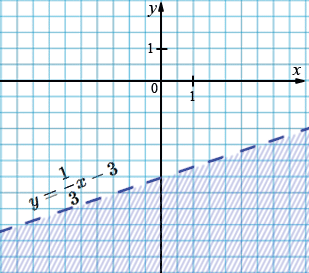
Пояснения:
Общие правила:
1) Неравенства вида \(y \ge kx + b\) или \(y \le kx + b\) задают полуплоскости, ограниченные прямой \(y = kx + b\).
2) Если знак строгий (\(<\) или \(>\)), прямая не принадлежит множеству решений.
3) Если знак нестрогий (\(\le\) или \(\ge\)), прямая входит в множество решений.
4) Чтобы определить, какую сторону от прямой заштриховывать, можно подставить любую точку, не лежащую на прямой, например \((0;0)\), если она не лежит на границе.
В учебнике требуется построение графиков, поэтому на координатной плоскости нужно провести каждую прямую и отметить соответствующую полуплоскость.
Вернуться к содержанию учебника