Упражнение 451 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 134

а) \(x \ge 3\)

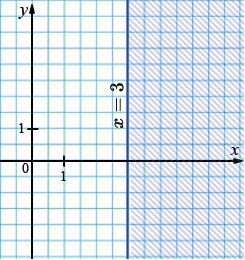
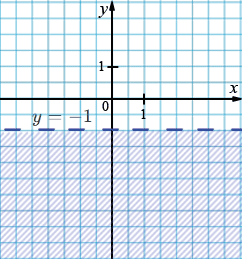
б) \(y < -1\)

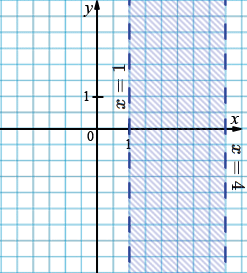
в) \(1 < x < 4\)

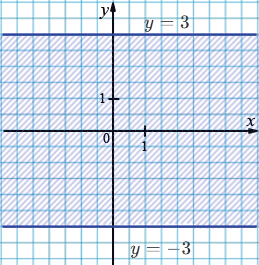
г) \(-3 \le y \le 3\)

Пояснения:

Общие правила:

1) Неравенство вида \(x \ge a\) задаёт вертикальную полуплоскость.

2) Неравенство вида \(y < b\) задаёт горизонтальную полуплоскость.

3) Двойные неравенства, такие как \(1 < x < 4\), задают полосу между двумя параллельными прямыми.

4) Нестрогий знак (\(\le\), \(\ge\)) означает включение границы, строгий — исключение.

Пояснение к пункту а)

Неравенство \(x \ge 3\) означает, что все подходящие точки находятся на прямой \(x = 3\) и правее её. Это правая полуплоскость, включая границу.

Пояснение к пункту б)

Неравенство \(y < -1\) описывает всю область ниже прямой \(y = -1\). Прямая не включена.

Пояснение к пункту в)

Двойное неравенство \(1 < x < 4\) задаёт вертикальную полосу между прямыми \(x = 1\) и \(x = 4\), но сами прямые не входят в решение.

Пояснение к пункту г)

Неравенство \(-3 \le y \le 3\) задаёт горизонтальную полосу между прямыми \(y = -3\) и \(y = 3\), включая обе границы.