Упражнение 319 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 105
Вернуться к содержанию учебника
Вопрос
Решите уравнение \(x^3 = x\) двумя способами: графическим и аналитическим.
Подсказка
Вспомните:
- Приемы решения целых уравнений.
- Разложение многочленов на множители.
- Разность квадратов двух выражений.
- Свойства умножения.
- Линейная функция, ее график.
- График функции \(y = x^3\).
- Координаты точки.
- Линейное уравнение с одной переменной.
Ответ
\(x^3 = x\)
Графический способ
\(y = x^3\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
\(y = x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
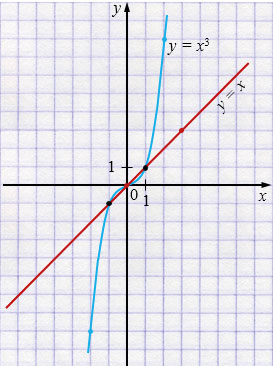
Точки пересечения графиков:
\((-1;\,-1),\; (0;\,0),\; (1;\,1)\).
\(x = -1,\; 0,\; 1\) - корни уравнения.
Аналитический способ
\(x^3 = x\)
\(x^3 - x = 0\)
\(x(x^2 - 1) = 0\)
\(x(x - 1)(x + 1) = 0\)
или \(x = 0\)
или \(x - 1 = 0\)
\(x = 1\)
или \(x + 1 = 0\)
\(x = -1\)
Ответ: \(-1; \, 0; \,1\).
Пояснения:
Графический способ
Чтобы решить графически уравнение \(x^3 = x\), нужно найти точки пересечения двух графиков:
\(y = x^3\) и \(y=x\), где
\(y = x^3\) - кубическая функция, графиком которой является кубическая парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y= x\) - линейная функция, графиком является прямая. Строят график по двум точкам.
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
Аналитический способ
Переносим все члены в одну часть, чтобы получить многочлен в левой части уравнения: \[ x^3 - x = 0. \] Выносим общий множитель \(x\): \[ x(x^2 - 1) = 0. \] Выражение в скобках — разность квадратов: \[x(x - 1)(x + 1) = 0. \] Произведение равно нулю, когда хотя бы один множитель равен нулю, значит: \[ x = 0,\quad x - 1 = 0,\quad x + 1 = 0. \] Отсюда получаем три корня: \[ x = 0,\quad x = 1,\quad x = -1. \]
Итак, оба способа дают один и тот же набор корней: \[ x = -1,\; 0,\; 1. \]
Вернуться к содержанию учебника