Упражнение 320 - ГДЗ по Алгебре 9 класс Макарычев, Миндюк учебник. Страница 105

С помощью графиков выясните, сколько решений может иметь уравнение \(x^3 + ax + b = 0\) при различных значениях \(a\) и \(b\).

Вспомните:

\(x^3 + ax + b = 0\)

\(x^3= -ax - b\)

\(y = x^3\)

\(x\)	-2	-1	0	1	2
\(y\)	-8	-1	0	1	8

\(y = -ax - b\) - прямая.

1) Если \(a = 0\), \(b\) - любое число,

то прямая параллельна оси \(x\).

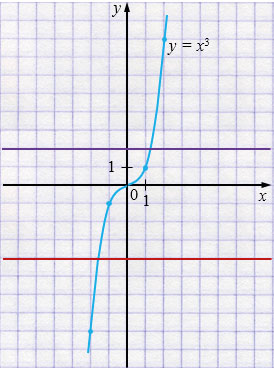
1 решение.

2) Если \(a > 0\), \(b\) - любое число,

то прямая убывает.

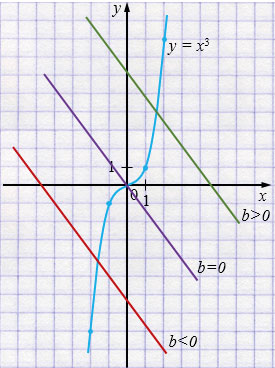
1 решение.

3) Если \(a > 0\), \(b\) - любое число,

то прямая возрастает.

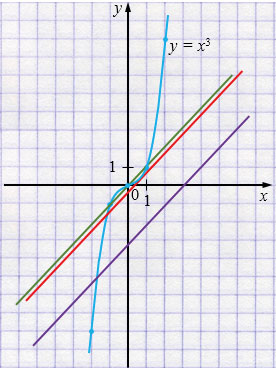
1 решение или 2 решения или 3 решения.

Упражнение 320 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 105