Упражнение 281 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 92

а) \(y = \sqrt{25 - x^2} + \sqrt{9x - x^2 - 14}\)

\( \begin{cases} 25 - x^2 \ge 0,\\ 9x - x^2 - 14 \ge 0 \end{cases} \)

1) \(25 - x^2 \ge 0\)

\(-x^2 + 25 \ge 0\)

\(y = - x^2 + 25\) - парабола, ветви которой направлены вниз.

\(25 - x^2 = 0\)

\(-x^2 = -25\)

\(x^2 = 25\)

\(x = \pm \sqrt{25}\)

\(x = \pm5\)

2) \(9x - x^2 - 14 \ge 0\)

\(-x^2 + 9x - 14 \ge 0\)

\(y = -x^2 + 9x - 14\) - парабола, ветви которой направлены вниз.

\(-x^2 + 9x - 14 = 0\)   \(/\times (-1)\)

\(x^2 - 9x + 14 = 0\)

\(D = (-9)^2 - 4\cdot 1\cdot 14= \)

\(= 81 - 56 = 25 > 0 \) - 2 корня.

\(x_1 = \frac{9 +5}{2\cdot1} = \frac{14}{2} = 7\).

\(x_2 = \frac{9 - 5}{2\cdot1} = \frac{4}{2} = 2\).

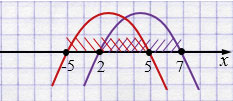
\(x \in [2;5]\)

Ответ: целые \(x\): \(2,3,4,5\).

б) \(y = \sqrt{8x - x^2 - 12} + \sqrt{16 - x^2}\)

\( \begin{cases} 8x - x^2 - 12 \ge 0,\\ 16 - x^2 \ge 0 \end{cases} \)

1) \(8x - x^2 - 12 \ge 0\)

\(-x^2 + 8x - 12 \ge 0\)

\(y = -x^2 + 8x - 12\) - парабола, ветви которой направлены вниз.

\(-x^2 + 8x - 12 = 0\)   \(/\times (-1)\)

\(x^2 - 8x + 12 = 0\)

\(D = (-8)^ - 4 \cdot1\cdot 12 =\)

\(=64 - 48 = 16 >0) - 2 корня.

\(\sqrt {16} = 4\).

\(x_1 = \frac{8+4}{2\cdot1} = \frac{12}{2} = 6\).

\(x_1 = \frac{8-4}{2\cdot1} = \frac{4}{2} = 2\).

2) \(16 - x^2 \ge 0\)

\(-x^2 + 16 \ge 0\)

\(y = -x^2 + 16\) - парабола, ветви которой направлены вниз.

\(-x^2 + 16 = 0\)

\(-x^2 = -16\)

\(x^2 = 16\)

\(x = \pm \sqrt{16}\)

\(x = \pm 4\)

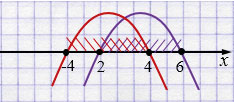
\(x \in [2; 4]\)

Ответ: целые \(x\): \(2,3,4\).

Пояснения:

В обоих пунктах под знаком квадратного корня стоят выражения. Чтобы функция была определена, каждое подкоренное выражение должно быть неотрицательно, то есть область определения функции задается системой неравенств и задание сводится поиску решения системы неравенств.

Решение системы неравенств — это пересечение множеств решений всех неравенств системы. Поэтому после нахождения промежутков для каждого неравенства мы строим их пересечение, как это сделано для пунктов а)–е).

Решение неравенств вида

\(ax^2 + bx + c \ge 0\) и \(ax^2 + bx + c \le 0\):

1) находим корни квадратного трехчлена \(ax^2 + bx + c\), если они есть;

2) если трехчлен имеет корни, то отмечаем их на оси \(x\) и через отмеченные точки проводим схематически параболу, ветви которой направлены вверх при \(a > 0\) или вниз при \(a < 0\); если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при \(a > 0\) или нижней при \(a < 0\);

3) находят на оси \(x\) промежутки, для которых точки параболы расположены выше оси \(x\) и на оси \(x\) (если решают неравенство \(ax^2 + bx + c \ge 0\)) или ниже оси \(x\) и на оси \(x\) (если решают неравенство \(ax^2 + bx + c \le 0\)).

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

Дискриминант квадратного трехчлена

\(ax^2 + bx + c \):

\(D = b^2 - 4ac\).

Если \(D > 0\), то квадратный трехчлен имеет 2 корня:

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\).

Если \(D = 0\), то квадратный трехчлен имеет 1 корень:

\(x = -\frac{b}{2a}\).

Если \(D < 0\), то квадратный трехчлен не имеет корней.

Корни уравнения \(ax^2 + bx\) находим разложением многочлена на множители \(x(ax + b)\) и используем то, что произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю: \(x = 0\)  или \(ax + b = 0\), откуда \(x = -\frac{b}{a}\).

Чтобы найти корни уравнения \(ax^2 + c = 0\), переносим коэффициент \(c\) в правую сторону: \(ax^2  = -с\), затем делим обе части уравнения на \(a\): \(x^2  = \frac{-с}{a}\), откуда получаем \(x_1 = -\sqrt{\frac{-c}{a}}\) и \(x_2= \sqrt{\frac{-c}{a}}\).

Из промежутков, являющихся решениями системы, выписываем целые значения, включая крайние точки промежутков.