Упражнение 79 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 28

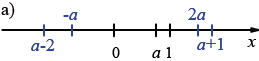
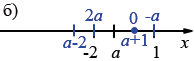
Пояснения:

Чтобы понять, где расположены точки, нужно опираться на свойства координатной прямой.

При  этом заметим, что на рис. а число \(a\) больше нуля и меньше единицы.  На на рис. б расстояние от \(a\) до \(1\), равно удвоенному расстоянию от \(-2\) до \(a\), следовательно, нуль находится посередине между \(a\) до \(1\), а значит, \(a=-1\).

1. Умножение координаты.

Если число умножается на 2, его точка на прямой отдаляется от нуля в 2 раза:

а) \(a>0;  2a > a \Rightarrow\) точка \(2a\) находится правее точки \(a\) на расстоянии  \(2a\) от нуля.

б)  \(a<0;  2a < a \Rightarrow\) точка \(2a\) находится левее точки \(a\) и совпадает с точкой \(-2\).

2. Противоположные числа.

Числа \(a\) и \(-a\) лежат по разные стороны от нуля и равноудалены от него:

3. Прибавление числа.

Добавление 1 смещает точку на одну единицу вправо:

\[ a + 1 > a. \]

4. Вычитание числа.

Вычитание 2 смещает точку на две единицы влево:

\[ a - 2 < a. \]