Упражнение 1027 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(\dfrac{a}{b}=\dfrac{c}{d}\),

\(a >0, b>0, c>0, d>0\)

\(a > b, a > c, a > d\)

Доказать:

\[ a+d>b+c. \]

Доказательство:

Пусть \(\dfrac{a}{b}=\dfrac{c}{d}=k\) и ( \(k>1\) ), так как \(a > b\), тогда

\( a=kb,\qquad c=kd. \)

\(a+d>b+c \)

\(a+d-b-c >0 \)

\(kb+d-b-kd >0 \)

\((kb-b)-(kd - d) >0 \)

\(b(k-1)-d(k - 1) >0 \)

\((k-1)(b-d) > 0\)

1) \(k - 1 > 0\), так как \(k > 1\).

2) \(\dfrac{a}{b}=\dfrac{c}{d} = k > 1\) и \(a\) - наибольшее число, поэтому \(b > d\), значит,

\(b - d > 0\), тогда неравенство

\((k-1)(b-d) > 0\) - верно и

\( a+d>b+c. \) Что и требовалось доказать.

Пояснения:

При доказательстве неравенства

\(a+d>b+c \), находим разность левой и правой частей неравенства и учитываем то, что, если \(a - b > 0\), то \(a > b\).

Также вводим коэффициент

\(k = \dfrac{a}{b}=\dfrac{c}{d}\), причем \(k > 1\), так как \(a > b\) по условию. Тогда получаем \( a=kb,\; c=kd \) и из неравенства

\(a+d>b+c \) получаем неравенство \((k-1)(b-d) > 0\), которое является верным неравенством, так как

\(k - 1 > 0\), учитывая то, что \(k > 1\), и 

\(b - d > 0\), учитывая то, что

\(\dfrac{a}{b}=\dfrac{c}{d} = k > 1\), при этом \(a\) - наибольшее число, поэтому \(b > d\). Следовательно, \( a+d>b+c. \) Что и требовалось доказать.

а) \( \begin{cases} 3x > 40{,}8,   /: 3 \\ 5x - a < 0 \end{cases} \)

\( \begin{cases} x > \frac{40{,}8}{3}, \\ 5x  < a    / : 5 \end{cases} \)

\( \begin{cases} x > 13,6, \\ x  < \frac{a}{5}    / : 5 \end{cases} \)

Система не имеет решений, например, при \(a = 10\)

\( \begin{cases} x > 13,6, \\ x  < \frac{10}{5} \end{cases} \)

\( \begin{cases} x > 13,6, \\ x  < 2 \end{cases} \)

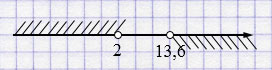
Ответ: при \(a = 10\) система не имеет решений.

б) \( \begin{cases} 1 - 6x < 19, \\ 4x - a < 6 \end{cases} \)

\( \begin{cases} - 6x < 19-1, \\ 4x < 6+a \end{cases} \)

\( \begin{cases} - 6x < 18,   / : (-6) \\ 4x < 6+a  / : 4 \end{cases} \)

\( \begin{cases} x > -3, \\ x < \frac{6+a}{4} \end{cases} \)

Ответ: натуральных значений \(a\), при которых система не имеет решений, не существует.

Пояснения:

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.