Упражнение 963 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\((k-4)x^2 + 16x - 24 = 0\).

\(A = k-4,\; B = 16,\; C = -24\).

\(k-4 \neq 0 \)

\(k \neq 4\).

\(D = B^2 - 4AC =\)

\(=16^2 - 4(k-4)(-24)=\)

\( = 256 - 4(k-4)(-24)=\)

\( = 256 + 96(k-4)=\)

\( = 256 + 96k - 384=\)

\( = 96k - 128\).

Уравнение имеет два корня при \(D > 0\).

\(96k - 128 > 0\)

\(96k > 128\)   \(/ : 96\)

\(k > \frac{128}{96}\)

\(k > \frac{4}{3}\)

\(k > 1\frac{1}{3}\).

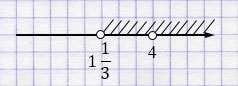
Ответ: \( (1\frac{1}{3}; 4) \cup (4; +\infty)\).

Пояснения:

Для квадратного уравнения \(Ax^2 + Bx + C = 0\) количество корней определяется дискриминантом:

\[D = B^2 - 4AC\]

- \(D > 0\) — два различных корня;

- \(D = 0\) — один корень;

- \(D < 0\) — нет корней.

Кроме того, уравнение должно оставаться квадратным, поэтому

\(A \neq 0\), что выполняется при \(k \neq 4\).

В задаче получили дискриминант

\(D = 96k - 128\). Для двух корней необходимо \(D > 0\), то есть

\(96k - 128 > 0\).

При решении неравенства использовали то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Решив неравенство, получили \(k > 1\frac{1}{3}\). Значит, множество значений параметра \(k\), при которых уравнение имеет два корня определяется объединением промежутков \( (1\frac{1}{3}; 4) \cup (4; +\infty)\).

Пусть длина половины пути равна \(S\) км, а скорость на второй половине пути равна \(x\) км/ч (\(x > 60\)).

Средняя скорость не превышала \(72\) км/ч:

\(\frac{S + S}{\frac{S}{60} + \frac{S}{x}} \le 72\)

\(\frac{2\cancel S}{\cancel S(\frac{1}{60} + \frac{1}{x})} \le 72\)

\(\frac{2}{\frac{1}{60} + \frac{1}{x}} \le 72\)

Составим систему неравенств:

\(\begin{cases} \dfrac{2}{\frac{1}{60} ^{\color{blue}{\backslash x}} + \frac{1}{x} ^{\color{blue}{\backslash 60}}} \le 72,\\ x > 60 \end{cases} \)

\(\begin{cases} \dfrac{2}{\frac{x + 60}{60x}} \le 72,\\ x > 60 \end{cases} \)

\(\begin{cases} \dfrac{2\cdot60x}{x + 60} \le 72,   /\times (x + 60)\\ x > 60 \end{cases} \)

\(\begin{cases} 120x \le 72(x + 60), \\ x > 60 \end{cases} \)

\(\begin{cases} 120x \le 72x + 4320, \\ x > 60 \end{cases} \)

\(\begin{cases} 120x - 72x \le 4320, \\ x > 60 \end{cases} \)

\(\begin{cases} 48x \le 4320,  / : 48 \\ x > 60 \end{cases} \)

\(\begin{cases} x \le 90, \\ x > 60 \end{cases} \)

\(x \in (60; 90]\)

Ответ: скорость во второй половине пути могла быть более \(60\) км/ч, но не более \(90\) км/ч.

Пояснения:

Чтобы найти среднюю скорость движения, нужно весь пройденный путь разделить на все время движения.

Обозначив длину половины пути через \(S\) км, а скорость на второй половине пути через \(x\) км/ч, составили систему неравенств, учитывая то, что средняя скорость на всём участке не превышала 72 км/ч, а скорость на втором участке пути больше \(60\) км/ч.

При решении системы неравенств используем то, что

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.